算法分析基础题目
第一章-算法概述
- 递归算法必须具备的两个条件是
<u>边界条件或停止条件</u>和<u>递推方程或递归方程</u> - 冒泡排序时间复杂度是___,堆排序时间复杂度是___。 ,
- 斐波那契数列的第1项为1,第2项为2,以后每一项等于前面两项之和,则第6项为
<u>13</u> - 算法分析主要是分析算法的性能,包括时间复杂度和
<u>空间复杂度</u> - 请求解递归式:n>1时,T(n)=2T(n/2)+n,否则T(n)=1,则其θ形式,T(n)=
<u>θ(nlogn)</u> - 以下递归程序fun(5,0)输出的第一个元素是
<u>1</u>,求解过程中最大层次为<u>4</u>
def fun(i,d):
if(i>1 and i%2!=0): fun(i-i//2,d+1)
if(i>1): fun(i//2,d+1)
- 求
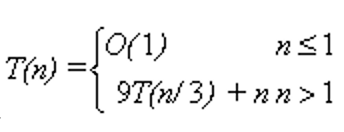 递推方程的解是
递推方程的解是 - 求递推方程
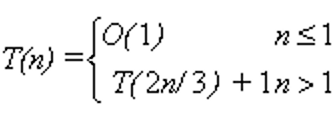 得到的解是
得到的解是 - 求递推方程
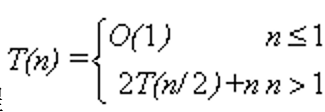 得到的解是
得到的解是 - bubble_sort最好情况下的时间复杂度,最坏情况下的时间复杂度为
第二章-分治法
-
有关以下代码,说法正确的是(ABCE)
def BinarySearch(s, x, low, high):
if (low > high):
return -1
middle = (low + high) / 2
if (x == s[middle]):
return middle
elif(x > s[middle]):
return BinarySearch(s, x, middle + 1, high)
else :
return BinarySearch(s, x, low, middle - 1)A.BinarySearch的功能是针对有序序列s[] ,采用二分搜索技术查找指定元素x.
B.if (low>high) return -1;该语句为递归的边界条件。
C.将问题规模一份为二的语句是middle=(low+high)/2;
D.递归序列左半部分的语句是BinarySearch (s, x, middle+1, high);
E.递归序列左半部分的语句是BinarySearch (s, x, low, middle-1);
-
以下问题中,哪些问题的分治算法消耗的时间与输入序列无关.(BD)
A.二分查找
B.合并排序
C.快速排序
D.最小值问题
-
填写以下二分搜索的代码中空缺的部分。(low+high)/2
def BinarySearch(s, x, low, high):
if (low > high):
return -1
middle = ___; //分解
if (x == s[middle]):
return middle
elif(x > s[middle]):
return BinarySearch(s, x, middle + 1, high)
else :
return BinarySearch(s, x, low, middle - 1) -
n个元素中找第二大元素的分治算法时间复杂度的是
-
根据下面斐波那契数列的递归算法,可知斐波那契数列递推方程的停止条件是
<u>n=0或n=1</u>。
def Fibonacci(int num):
if(num == 0 || num == 1):return num
return Fibonacci(num-1)+Fibonacci(num - 2)
-
下面代码为求n!的递归算法,该代码反应的n!问题递归实现的停止条件(边界条件)为
<u>当n=1时n!=1</u>。def fun(n):
if (n == 1):
return 1
else :
return fun(n - 1) * n -
对可排序的序列s[left:right]进行合并排序,其分治算法分解操作为mid = (left+right)//2,得到的两个子问题序列是
<u>s[left:mid],s[mid+1,right]</u> -
2k×2k的棋盘覆盖问题,用k表示问题的规模,则时间复杂度为
<u>O(4k)</u>。 -
线性时间选择问题寻找基准元素的方法是
<u>将n个元素按照5个元素一组进行分组,取每组的中位数,然后再取中位数的中位数作为基准</u> -
4个运动员的循环赛日程表算法安排的结果是
<u>第一天1-2,3-4,第二天1-3,2-4,第三天:1-4,2-3</u>
第3章-回溯法
-
有关图的m着色问题说法正确的是(AC)
A.该问题的解形式为(x1,x2,…,xn),xi表示第i个顶点着xi号色,其取值范围为:令为颜色集合,则xi∈S
B.该问题的解空间的组织结构是排列树。
C.该问题需要设置约束条件,不需要限界条件。
D.该问题不需要设置约束条件,只需要限界条件。
E.该问题既需要设置约束条件,也需要限界条件。
- 有关最小重量机器设计问题说法正确的是(BE)
A.该问题的解形式为(x1,x2,…,xn),xi取值范围为:令,则
B.该问题的解空间的组织结构是满m叉树。
C.该问题需要设置约束条件,不需要限界条件。
D.该问题不需要设置约束条件,只需要限界条件。
E.该问题既需要设置约束条件,也需要限界条件。
-
n皇后问题的解的形式定义为(x1,x2,...,xn),其中,xi(i=1,2,...,n)的取值为1,2....,n,则它的解空间的组织结构为一棵 _ 树。如果,,则对应的解空间树是一棵_树 ,答案:
<u>满n叉树</u>、<u>排列树</u> -
0-1背包问题的解的形式定义为(x1,x2,...,xn),其中,xi(i=1,2,...,n)的取值为0或1,则它的解空间的组织结构为一棵 ___。答案:子集树
-
最大团问题的解的形式定义为(x1,x2,...,xn),其中,xi(i=1,2,...,n)的取值为0或1,则它的解空间的组织结构为一棵 ___。答案:子集树
-
旅行售货员问题的解的形式定义为(x1,x2,...,xn),其中,xi(i=1,2,...,n)的取值,则它的解空间的组织结构为一棵 ___。答案:排列树
-
图的m着色问题的解的形式定义为(x1,x2,...,xn),其中,xi(i=1,2,...,n)的取值为1,2....,m,则它的解空间的组织结构为一棵 ___ 树。答案:满m叉树
-
最小重量机器设计问题的解的形式定义为(x1,x2,...,xn),其中,xi(i=1,2,...,n)的取值为1,2....,m,则它的解空间的组织结构为一棵树,深度是___(默认根结点深度为0)。答案:满m叉树
-
回溯法采用的搜索方式是___。答案:深度优先
-
回溯法是一种能进则 __,进不了则___,换不了则___的搜索算法。答案:进、换、退或回
第4章-动态规划
-
有关0-1背包问题,用c[i][j]描述子问题:1...i共i个物品,背包容量为j的最优值(装入背包的最大价值),则其子问题为:1...i-1共i-1个物品,背包容量为j-w ix i,以下说法正确的是(ABD)
A.当i=0时或j=0时,c[i][j]=0。
B.当
j<w i时,物品无法装入,其x i=0,则背包容量依旧为j,c]i][j]=c[i-1][j].C.当
j≥w i时,物品可以装入,装呢还是不装呢?这取决于哪个决策能够让c[i][j]最小。故c]i][j]=min(c[i-1][j],c[i-1][j-w i]+v i)D.当
j≥w i时,物品可以装入,装呢还是不装呢?这取决于哪个决策能够让c[i][j]最大。故c]i][j]=max(c[i-1][j],c[i-1][j-w i]+v i) -
有关最优二叉搜索树说法正确的是(ABD)
A.优二叉搜索树的左孩子的节点都比根节点小,右孩子节点都比根节点大。
B.最优二叉搜索树的平均比较次数最少。
C.最优二叉搜索树的平均比较次数最多。
D.最优二叉搜索树中有n个是节点,n+1个虚节点。
-
,虚节点的最优二叉搜索树问题的子问题描述为有序序列,虚节点的最优二叉搜索树,以下描述正确的是(ABC)。
A.i=1,j=n表示规模为n的原问题。
B.i=j+1,表示字符序列为空,对应的最优二叉搜索树为一棵空树。
C.有序序列,虚节点的最优二叉搜索树的子问题是:有序序列,虚节点的最优二叉搜索树和有序序列,虚节点的最优二叉搜索树。
D.子问题的最优值:最小平均比较次数c[i][j],左子树的最优值:最小平均比较次数c[i][k-1],右子树的最优值:最小平均比较次数c[k+1][j],三者之间的关系为:c[i][j]=c[i][k-1]+c[k+1][j]+pi+...+pj+qi-1+...+qj
-
有关最长公共子序列问题的动态规划算法说法正确的是(AB)
A.X n和Y m的代表了两个长度为n和m的字符串,求X n和Y m的最长公共子序列的子问题是:求X i和Y j的最长公共子序列,i=0,1,...n,j=0,1,...,m。
B.X i和Y j的最长公共子序列当i=0时,最长公共子序列的长度为0;j=0时,最长公共子序列的长度也为0。
C.设X i和Y j的最长公共子序列的长度c[i][j],求最优值的递归关系式为
i[j]=c[i-1][j]。D.设X i和Y j的最长公共子序列的长度c[i][j],求最优值的递归关系式为
i[j]=c[i-1][j]+1。 -
矩阵连乘问题中有多个矩阵相乘,问题是安排矩阵相乘的先后顺序,使总乘法次数最少,例如 有[A][B]C三个矩阵,则可行的顺序有ABC\ACB\CAB\CBA\BAC\BCA六个。 答案:否
-
以动态规划求解0-1背包问题,背包容量可以是任意实数。 答案:否
-
最长公共子序列问题中,如果采取穷举法,可以在序列A中子序列可能的开头和结尾(因为子序列由其开头位置和结尾位置唯一确定),然后在序列B中查找它是否存在,如果按照子序列长度降序枚举,找到的第一个公共子序列就是最长公共子序列。答案:否
-
0-1背包问题的动态规划解法不适合背包容量非常大(
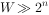 )的情况。答案:是
)的情况。答案:是 -
最长公共子序列问题的动态规划解法时间复杂度等于两个序列长度之积。答案:是
- 0-1背包问题的贪心法解法和动态规划解法都能够生成最优解。答案:否
第5章-贪心算法
- 贪心算法的贪心策略确定后可以更改() 答案:否
- 针对同一个问题,贪心策略可能有多个,贪心算法��的好坏取决于贪心策略的好坏。 答案:是
- 一个好的贪心策略,肯定能得到问题的最优解。答案:否
- 贪心法具有高效性,它可以非常迅速地获得一个解。答案:是
- 找零钱问题一定能使得找出去的钱币数最少。答案:否
- 最优装载问题的贪心策略一定能使得装上船的集装箱个数最多。 答案:是
- 调度问题的贪心策略不一定能使得n个任务的总等待时间(总完成时间和)最短。 答案:否
- 会场安排的最佳贪心策略一定能保证安排最多的相容会议使用同一会议室。答案:是
- 物品可以切割的背包问题的最佳贪心策略不一定能保证装入背包的物品总价值最大。答案:否
- 堆排序、冒泡排序、快速排序都采用了贪心策略进行排序,答案:否
第6章-分支限界法
-
部落卫队问题。原始部落byteland中的居民们为了争夺有限的资源,经常发生冲突。几乎每个居民都有他的仇敌。部落酋长为了组织一支保卫部落的队伍,希望从部落的居民中选出最多的居民入伍,并保证队伍中任何2 个人都不是仇敌。给定byteland部落中居民间的仇敌关系,编程计算组成部落卫队的最佳方案。以下有关部落卫队问题说法正确的是(ACDE)
A.该问题的解的形式为(x1,x2,...,x3),xi(i-1,2,3,...,n)=0或1,0表示居民未被选入部落卫队,1表示居民被选入部落卫队。
B.该问题的解空间组织结构为一棵排列树,规模为n时,树的深度为n。
C.该问题可以用分支限界法求解,也可以用回溯法求解。
D.该问题需要设置约束条件,也需要设置限界条件。
E.将给定的仇敌关系图转换成它的补图,则成为友好关系图,部落卫队问题实质就是最大团问题。
-
分支限界法和回溯法都是搜索法,但它们的搜索方式是不同的,分支限界法是以深度优先搜索的方式进行搜索,而回溯法是以广度优先的方式进行搜索,答案:否
-
分支限界法是一种“能进则进、进不了则换、换不了则退(回溯)”的搜索方法。答案:否
-
分支限界法有两种类型:队列式分支限界法和优先队列式分支限界法 答案:是
-
分支限界法的扩展方式为一次生成所有的孩子节点 答案:是
-
分支限界法搜索过程中保留下来的结点即为活结点,是符合约束条件的可能导致最优解的结点 答案:否
-
分支限界法搜索过程中,舍弃的是导致不可行解的结点和导致非最优解的结点 答案:是
-
分支限界法的求解目标则是找出满足条件的一个解。回溯法的求解目标是找出解空间树中满足条件的所有解。 答案:是
-
0-1背包问题可以用队列式分支限界法,也可以用优先队列式分支限界法求解。 答案:是
-
优先队列式分支限界法搜索过程中使用的活结点表可以用堆或优先队列等数据结构实现。 答案:是