7月10日到16日做题实况

并查集-MinOr Tree

链接：https://www.luogu.com.cn/problem/CF1624G

题面翻译

给定 $n$ 个点， $m$ 条边 $(3 \le n \le 2 \times 10^5,n - 1 \le m \ \le 2 \times 10^5)$ , 求在或运算下的最小生成树。

保证图联通。

题目描述

Recently, Vlad has been carried away by spanning trees, so his friends, without hesitation, gave him a connected weighted undirected graph of $n$ vertices and $m$ edges for his birthday.

Vlad defined the ority of a spanning tree as the bitwise OR of all its weights, and now he is interested in what is the minimum possible ority that can be achieved by choosing a certain spanning tree. A spanning tree is a connected subgraph of a given graph that does not contain cycles.

In other words, you want to keep $n-1$ edges so that the graph remains connected and the bitwise OR weights of the edges are as small as possible. You have to find the minimum bitwise OR itself.

输入格式

The first line of the input contains an integer $t$ ( $1 \le t \le 10^4$ ) — the number of test cases in the input.

An empty line is written in front of each test case.

This is followed by two numbers $n$ and $m$ ( $3 \le n \le 2 \cdot 10^5, n - 1 \le m \le 2 \cdot 10^5$ ) — the number of vertices and edges of the graph, respectively.

The next $m$ lines contain the description of the edges. Line $i$ contains three numbers $v_i$ , $u_i$ and $w_i$ ( $1 \le v_i, u_i \le n$ , $1 \le w_i \le 10^9$ , $v_i \neq u_i$ ) — the vertices that the edge connects and its weight.

It is guaranteed that the sum $m$ and the sum $n$ over all test cases does not exceed $2 \cdot 10^5$ and each test case contains a connected graph.

输出格式

Print $t$ lines, each of which contains the answer to the corresponding set of input data — the minimum possible spanning tree ority.

样例输入 #1

样例输出 #1

2
10
3

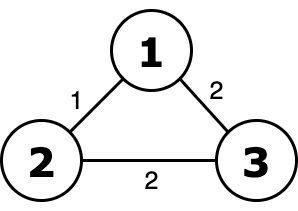Graph from the first test case. 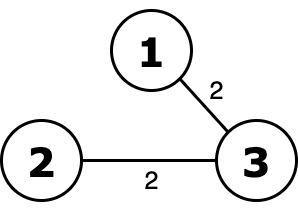Ority of this tree equals to 2 or 2 = 2 and it's minimal. 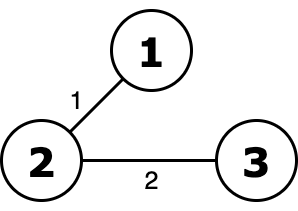Without excluding edge with weight $1$ ority is 1 or 2 = 3.

思路

考虑二进制拆位，如果第 $i$ 位可以为0，那么一定会比第 $i$ 位为1更优，不管后面位是什么。因此可以从高位向低位进行贪心选择这一位是1还是0。

如何check选1还是选0？

如果第 $i$ 位可以放0，那么，所有选的边权里面的第 $i$ 位都要是0，

可以使用并查集，如果一个边 $w$ 满足条件：

$w$ 的第 $i$ 位必须为0： $w>>i\&0$
当前答案 $res$ 选过0的地方不可以出现1： $res|w<res+(1>>(k+1))$

那么就可以把这个边加入到最小生成树中，类似于克鲁思卡尔算法。

最后检查是否所有点都在一个集合中，在一个集合说明成立，这一位可以为0，否则为1

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

typedef struct edge {
    int x, y, w;
} edge;

void solve() {
    int n, m;
    cin >> n >> m;
    vector<edge> e(m + 1);
    for (int i = 1; i <= m; ++i) {
        int x, y, w;
        cin >> x >> y >> w;
        e[i] = {x, y, w};
    }
    vector<int> f(n + 1);
    auto find = [&](auto &find, int x) -> int {
        if (x != f[x]) f[x] = find(find, f[x]);
        return f[x];
    };
    auto solve = [&](int res, int k) -> bool {
        for (int i = 1; i <= n; ++i) f[i] = i;
        for (int i = 1; i <= m; ++i) {
            if ((e[i].w >> k) & 1) continue;
            if ((res | e[i].w) >= (res + (1ll << (k + 1))))continue;
            int xx = find(find, e[i].x);
            int yy = find(find, e[i].y);
            if (xx == yy) continue;
            f[xx] = yy;
        }
        bool ok = 1;
        for (int i = 2; i <= n; i++) {
            if (find(find, 1) != find(find, i)) {
                ok = 0;
                break;
            }
        }
        return ok;
    };
    int res = 0;
    for (int i = 32; i >= 0; i--) {
        if (!solve(res, i)) {
            res |= (1ll << i);
        }
    }
    cout << res << endl;
}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

并查集-MinOr Tree​

题面翻译​

题目描述​

输入格式​

输出格式​

样例输入 #1​

样例输出 #1​

思路​

代码​