RMQ
AcWing 1273. 天才的记忆
题目
给你一大串数字(编号为 1 到 N,大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 M 个询问,每次询问就给你两个数字 A,B要求你瞬间就说出属于 A 到 B 这段区间内的最大数。
思路
RMQ算法:使用动态规划预处理数据。
状态表示:f[i][j]表示以i为起点,长度为2^j的一段区间的最大值。
该区间的最大值可以先把这个区间[i,2^j-1]分成两半,最大值取两边的最大值,左区间为[i,i+2^(j-1)],右区间为:[i+2^(j-1),i+2^j-1]。
状态转移方程:f[i][j]=max(f[i,j-1],f[i+1<<(j-1)][j-1])
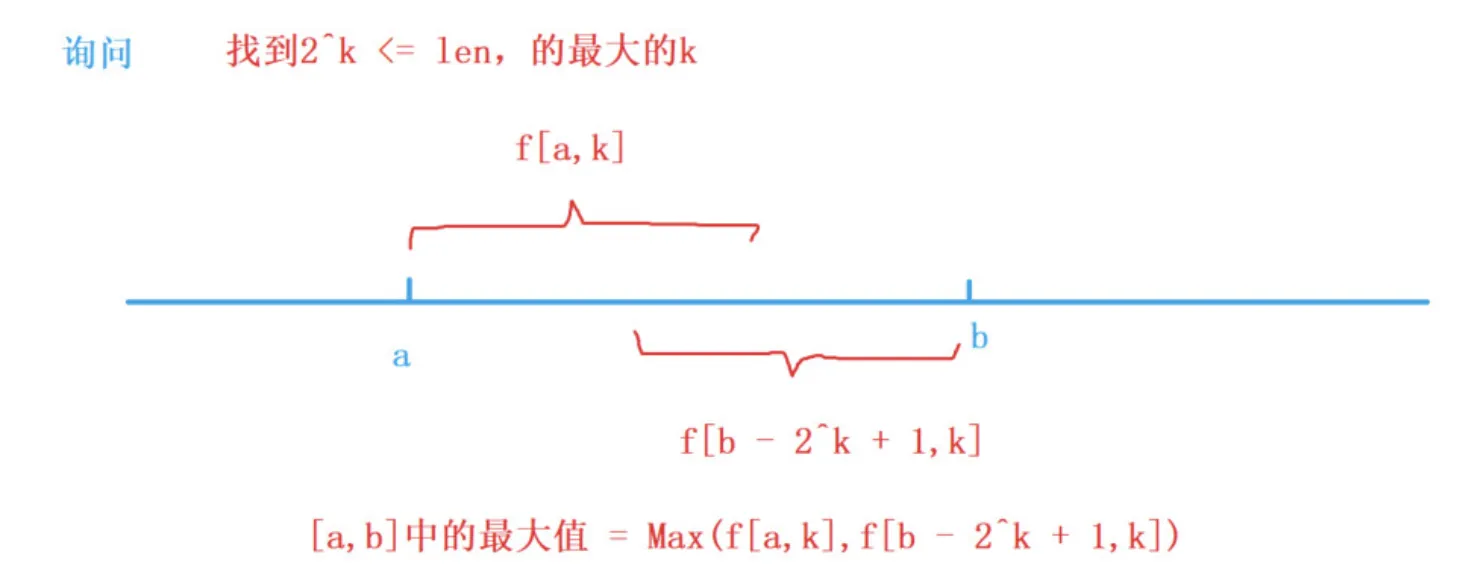
查询区间最大值:对于区间【l,r】,区间长度为r-l+1存在一个k使得2^k<=r-l+1,这个k的值为log2(r-l+1),则【l,l+2^k-1】和【r-2^k+1,r】可以覆盖整个区间。
区间最大值为:max(f[a,k],f[r-2^k+1][k])
代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define debug(x) printf("a[%d]=%d\n",x,a[x]);
#define pr(x) printf("x=%d\n",x);
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
typedef long long LL;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10;
int n,m;
int a[N];
int f[N][20];
void init(){
for(int j=0;j<20;j++){
for(int i=1;i+(1<<j)-1<=n;i++){
if (!j) f[i][j]=a[i];
else f[i][j]= max(f[i][j-1],f[i+(1<<j-1)][j-1]);
}
}
}
int query(int l,int r){
int k= log(r-l+1)/ log(2);
return max(f[l][k],f[r+1-(1<<k)][k]);
}
int main() {
IOS;
#ifndef ONLINE_JUDGE
freopen("/Users/houyunfei/CLionProjects/MyCppWorkSpace/test.in", "r", stdin);
freopen("/Users/houyunfei/CLionProjects/MyCppWorkSpace/test.out", "w", stdout);
#endif
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
init();
cin>>m;
while (m--){
int l,r;
cin>>l>>r;
cout<<query(l,r)<<endl;
}
return 0;
}