并查集
并查集介绍
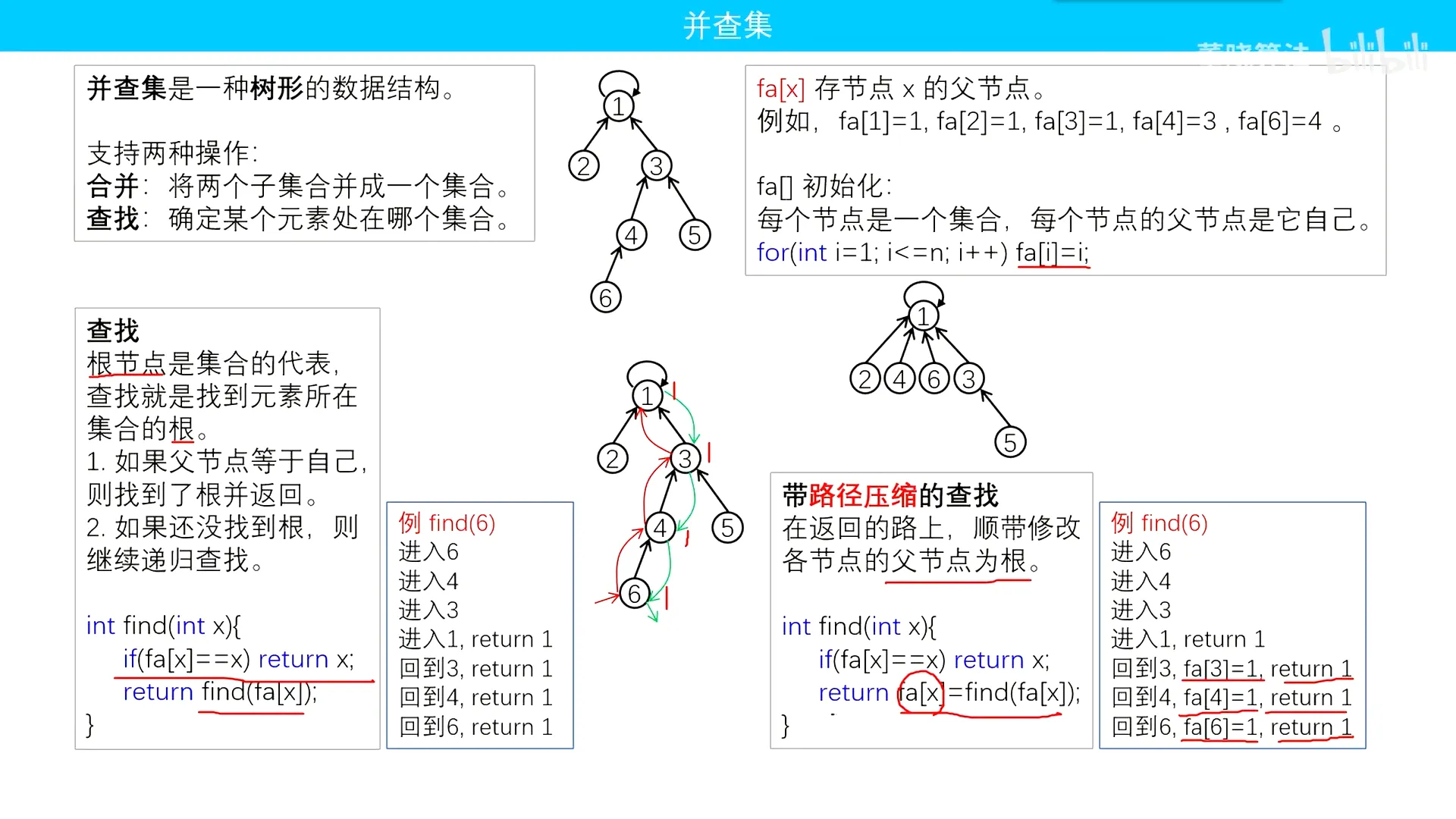
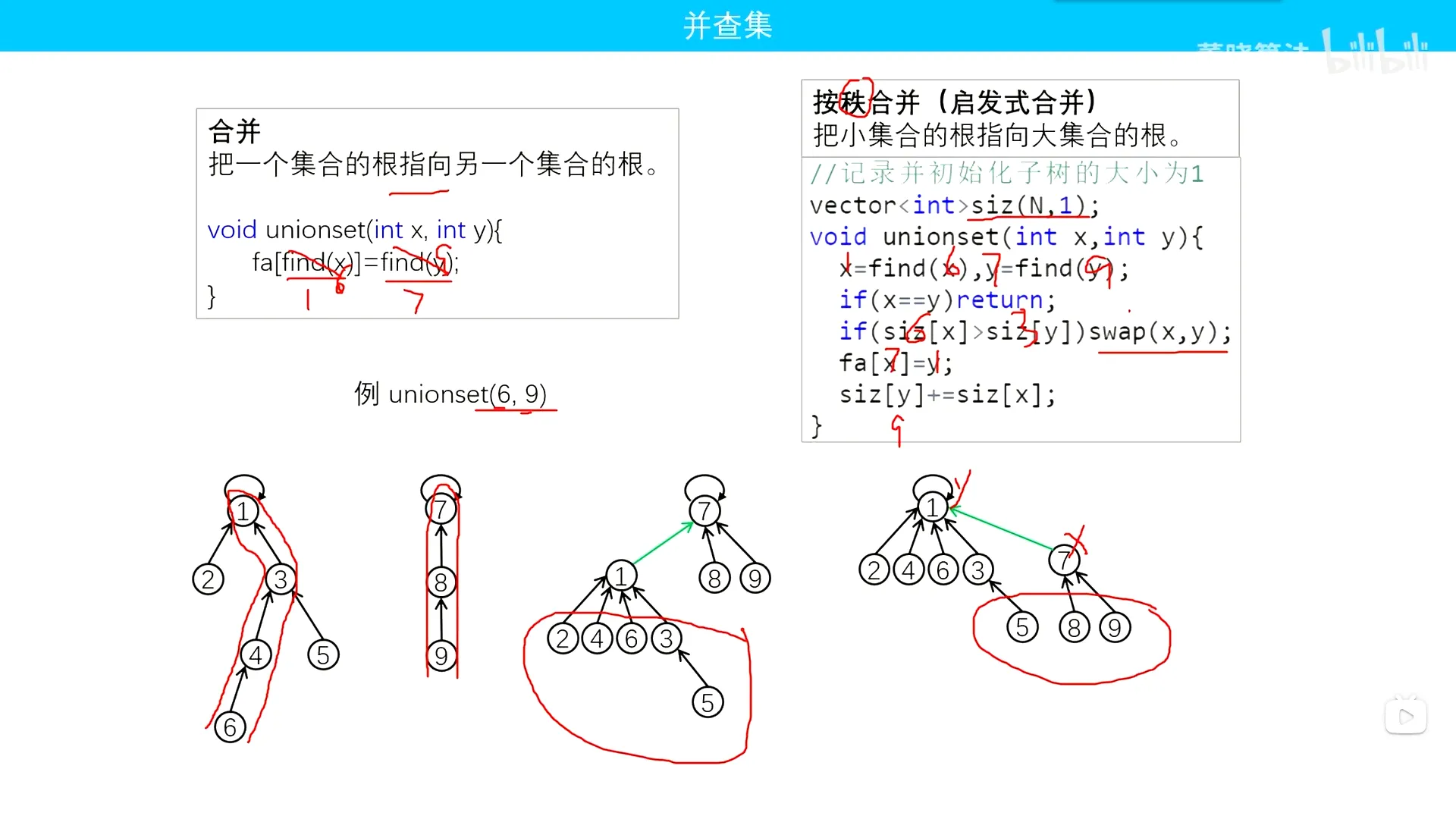
AcWing 1250. 格子游戏
题目
https://www.acwing.com/problem/content/1252/ Alice和Bob玩了一个古老的游戏:首先画一个 n×n 的点阵(下图 n=3 )。 接着,他们两个轮流在相邻的点之间画上红边和蓝边:
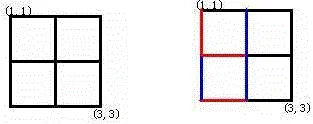
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了! 他们甚至在游戏中都不知道谁赢得了游戏。 于是请你写一个程序,帮助他们计算他们是否结束了游戏?
思路
并查集判断是否存在环:
- 将二维坐标一维化,并且从0开始,例如把(1,1)看成0,(1,2)看成1。。。把(x,y)看成
x*n+y - 根据是
D还是R,求出划线后终点的坐标 - 判断当前点的坐标和终点坐标是否在一个集合中,如果在一个集合中,说明形成环了,否则就合并他们
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N=40010;
int n,m;
int fa[N];
int find(int x)
{
if (fa[x]!=x) fa[x]= find(fa[x]);
return fa[x];
}
int get(int x,int y)
{
return x*n+y;
}
int main() {
cin>>n>>m;
for(int i=0;i<n*n;i++) fa[i]=i;//初始化并查集
char c;
int x,y,a,b;
for(int i=1;i<=m;i++)
{
cin>>x>>y>>c;
x--,y--;
a= get(x,y);
if (c=='D') b= get(x+1,y);
else b= get(x,y+1);
if (find(a)== find(b))
{
cout<<i<<endl;
return 0;
}
fa[find(a)]= find(b);
}
cout<<"draw"<<endl;
return 0;
}
AcWing 1252. 搭配购买
题目
https://www.acwing.com/problem/content/1254/ Joe觉得云朵很美,决定去山上的商店买一些云朵。 商店里有 n 朵云,云朵被编号为 1,2,…,n,并且每朵云都有一个价值。 但是商店老板跟他说,一些云朵要搭配来买才好,所以买一朵云则与这朵云有搭配的云都要买。 但是Joe的钱有限,所以他希望买的价值越多越好。
思路
- 将组合搭配的云朵看成是一个整体物品
- 用并查集将搭配的云朵合并集合,并维护
v[i] 和 w[i] - 对组合搭配的云朵做一遍 01 背包,即只有是根节点时才 dp
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N=10010;
int n,m,vol;
int v[N],w[N];
int p[N];
int f[N];
int find(int x)
{
if (p[x]!=x) p[x]= find(p[x]);
return p[x];
}
int main() {
cin>>n>>m>>vol;
for(int i=1;i<=n;i++) p[i]=i;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
while (m--)
{
int a,b;
cin>>a>>b;
int pa= find(a),pb= find(b);
if (pa!=pb)//不在一个集合中,就合并价值和体积
{
v[pa]+=v[pb];
w[pa]+=w[pb];
p[pb]=pa;
}
}
for(int i=1;i<=n;i++)
{
if (p[i]==i)
for(int j=vol;j>=v[i];j--)
{
f[j]= max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[vol]<<endl;
return 0;
}
AcWing 237. 程序自动分析
题目
https://www.acwing.com/problem/content/239/
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 x1,x2,x3,… 代表程序中出现的变量,给定 n 个形如xi=xj 或 xi≠xj的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。
例如,一个问题中的约束条件为:x1=x2,x2=x3,x3=x4,x1≠x4,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式 输入文件的第 1 行包含 1 个正整数 t,表示需要判定的问题个数,注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第 1 行包含 1 个正整数 n,表示该问题中需要被满足的约束条件个数。
接下来 n 行,每行包括 3 个整数 i,j,e,描述 1 个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 e=1,则该约束条件为 xi=xj;若 e=0,则该约束条件为 xi≠xj。
思路
离散化: 本题需要合并的数据很大,但是实际用到的数据只有2e5,可以进行离散化操作,然后去重 先处理相等的约束条件,进行并查集操作,合并在一个集合中, 再去处理不想等的条件,判断两个值是否在同一个并查集中。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N=200010;
int n,m;
int p[N];
unordered_map<int ,int >S;
struct Query
{
int x,y,e;
}query[N];
int get(int x)
{
if (S.count(x)==0) S[x]=++n;
return S[x];
}
int find(int x)
{
if (p[x]!=x) p[x]= find(p[x]);
return p[x];
}
int main() {
int t;
cin>>t;
while (t--)
{
n=0;
S.clear();
cin>>m;
for(int i=0;i<m;i++)
{
int x,y,e;
cin>>x>>y>>e;
query[i]={get(x), get(y),e};
}
for(int i=1;i<=n;i++) p[i]=i;
//合并相等的条件
for(int i=0;i<m;i++)
if (query[i].e==1)
{
int pa= find(query[i].x),pb= find(query[i].y);
p[pa]=pb;
}
//检查不相等条件
bool has_conflict=false;
for(int i=0;i<m;i++)
{
if (query[i].e==0)
{
int pa= find(query[i].x),pb= find(query[i].y);
if (pa==pb)
{
has_conflict=true;
break;
}
}
}
if (has_conflict) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
return 0;
}