数位DP

数字游戏

题目

链接：https://www.acwing.com/problem/content/1084/

科协里最近很流行数字游戏。

某人命名了一种不降数，这种数字必须满足从左到右各位数字呈非下降关系，如 $123$，$446$。

现在大家决定玩一个游戏，指定一个整数闭区间 $[a,b]$，问这个区间内有多少个不降数。

输入格式

输入包含多组测试数据。

每组数据占一行，包含两个整数 $a$ 和 $b$。

输出格式

每行给出一组测试数据的答案，即 $[a,b]$ 之间有多少不降数。

数据范围

$1 \le a \le b \le 2^{31}-1$

输入样例：

1 9
1 19

输出样例：

9
18

思路

状态表示：f[i][j]表示一共有i位，且最高位数字是j的不降数的个数

例如： j k x x x

最高位为j 次高位为k 应该满足 k>=j

状态转移：因为最高位已经固定为j了，所以假设第i-1位为k，根据不降数定义k>=j，所以$f[i][j]=\sum_{k=j}^{9}f[i-1][k]$

即：$f[i][j]=f[i-1][j]+f[i-1][j+1]+...+f[i-1][9]$

注意下面代码枚举j的时候是$<last$,而不是$=$

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 12;
int a[N];     //把整数的每一位数字抠出来，存入数组
int f[N][N];  //f[i][j]表示一共有i位，且最高位数字是j的不降数的个数

void init() {  //预处理不降数的个数
    for (int i = 0; i <= 9; i++) f[1][i] = 1;   //一位数
    for (int i = 2; i < N; i++) {               //阶段：枚举位数
        for (int j = 0; j <= 9; j++) {          //状态：枚举最高位
            for (int k = j; k <= 9; k++) {      //决策：枚举次高位
                f[i][j] += f[i - 1][k];
            }
        }
    }
}

int dp(int n) {
    if (n == 0) return 1;
    int cnt = 0;
    while (n) a[++cnt] = n % 10, n /= 10;

    int res = 0, last = 0;
    for (int i = cnt; i >= 1; i--) {
        int now = a[i];
        for (int j = last; j < now; j++) {
            res += f[i][j];
        }
        if (now < last) break;
        last = now;
        if (i == 1) res++;
    }
    return res;

}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    init();
    int l, r;
    while (cin >> l >> r) {
        cout << dp(r) - dp(l - 1) << endl;
    }
    return 0;
}

[SCOI2009] windy 数

https://www.luogu.com.cn/problem/P2657

题目背景

windy 定义了一种 windy 数。

题目描述

不含前导零且相邻两个数字之差至少为 $2$ 的正整数被称为 windy 数。windy 想知道，在 $a$ 和 $b$ 之间，包括 $a$ 和 $b$ ，总共有多少个 windy 数？

输入格式

输入只有一行两个整数，分别表示 $a$ 和 $b$。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1 10

样例输出 #1

9

样例 #2

样例输入 #2

25 50

样例输出 #2

20

提示

数据规模与约定

对于全部的测试点，保证 $1 \leq a \leq b \leq 2 \times 10^9$。

思路

区间转换：欲求$[a,b]$内Windy数的个数，先求$[0,x]$的Windy数的个数dp(x),答案即$dp(b)-dp(a-1)$。

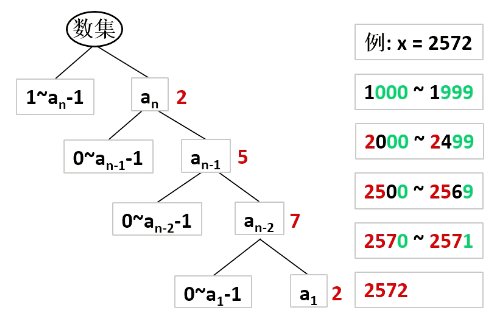
分类填数：设整数x一共n位，x表示为$a_n,a_{n-1},a_{n-2}…a_1$,从高位到低位枚举填数。 因为不含前导零，所以最高位只能填1~a,其他位可以填$0~a$。 每个位上填数时，分为两类：$0～a_i-1$和$a_i$,这样填数可以保证不超过x。

状态表示：f[i][j]表示一共有i位，且最高位数字为j的Windy数的个数

分段统计：

• 我们用last记录上一位数字，然后枚举当前位j，如果abs(j-last)>=2，就累加答案，$res+=f[i][j]$,这里统计的是n位的
• 对于位数低于n位的，累加到答案中即可

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 12;
int a[N];     //把整数的每一位数字抠出来，存入数组
int f[N][10]; //f[i][j]表示一共有i位，且最高位数字为j的Windy数的个数

void init() {
    for (int i = 0; i <= 9; i++) f[1][i] = 1;
    for (int i = 2; i < N; i++) {
        for (int j = 0; j <= 9; j++) {
            for (int k = 0; k <= 9; k++) {
                if (abs(j - k) >= 2) f[i][j] += f[i - 1][k];
            }
        }
    }
}

int dp(int n) {
    if (!n) return 0;
    int cnt = 0;
    while (n) a[++cnt] = n % 10, n /= 10;
    int res = 0, last = -2;
    for (int i = cnt; i >= 1; i--) { //答案为cnt位的
        int now = a[i];
        for (int j = (i == cnt); j < now; j++) {//最高位从1开始
            if (abs(j - last) >= 2) {
                res += f[i][j];
            }
        }
        if (abs(now - last) < 2) break;
        last = now;
        if (i == 1) res++;
    }
    for (int i = 1; i < cnt; i++) { //答案小于cnt位的
        for (int j = 1; j <= 9; j++) {
            res += f[i][j];
        }
    }
    return res;
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    init();
    int l, r;
    cin >> l >> r;
    cout << dp(r) - dp(l - 1);
    return 0;
}

树的度量

题目

求给定区间 $[X,Y]$ 中满足下列条件的整数个数：这个数恰好等于 $K$个互不相等的 $B$ 的整数次幂之和。

例如，设 $X = 15, Y = 20, K = 2, B = 2$，则有且仅有下列三个数满足题意：

$17 = 2^4 + 2^0$ $18 = 2^4 + 2^1$
$20 = 2^4 + 2^2$

输入格式

第一行包含两个整数 $X$ 和 $Y$，接下来两行包含整数 $K$ 和 $B$。

输出格式

只包含一个整数，表示满足条件的数的个数。

数据范围

$1 \le X \le Y \le 2^{31}-1$,
$1 \le K \le 20$ $2 \le B \le 10$

输入样例：

15 20
2
2

输出样例：

3

思路

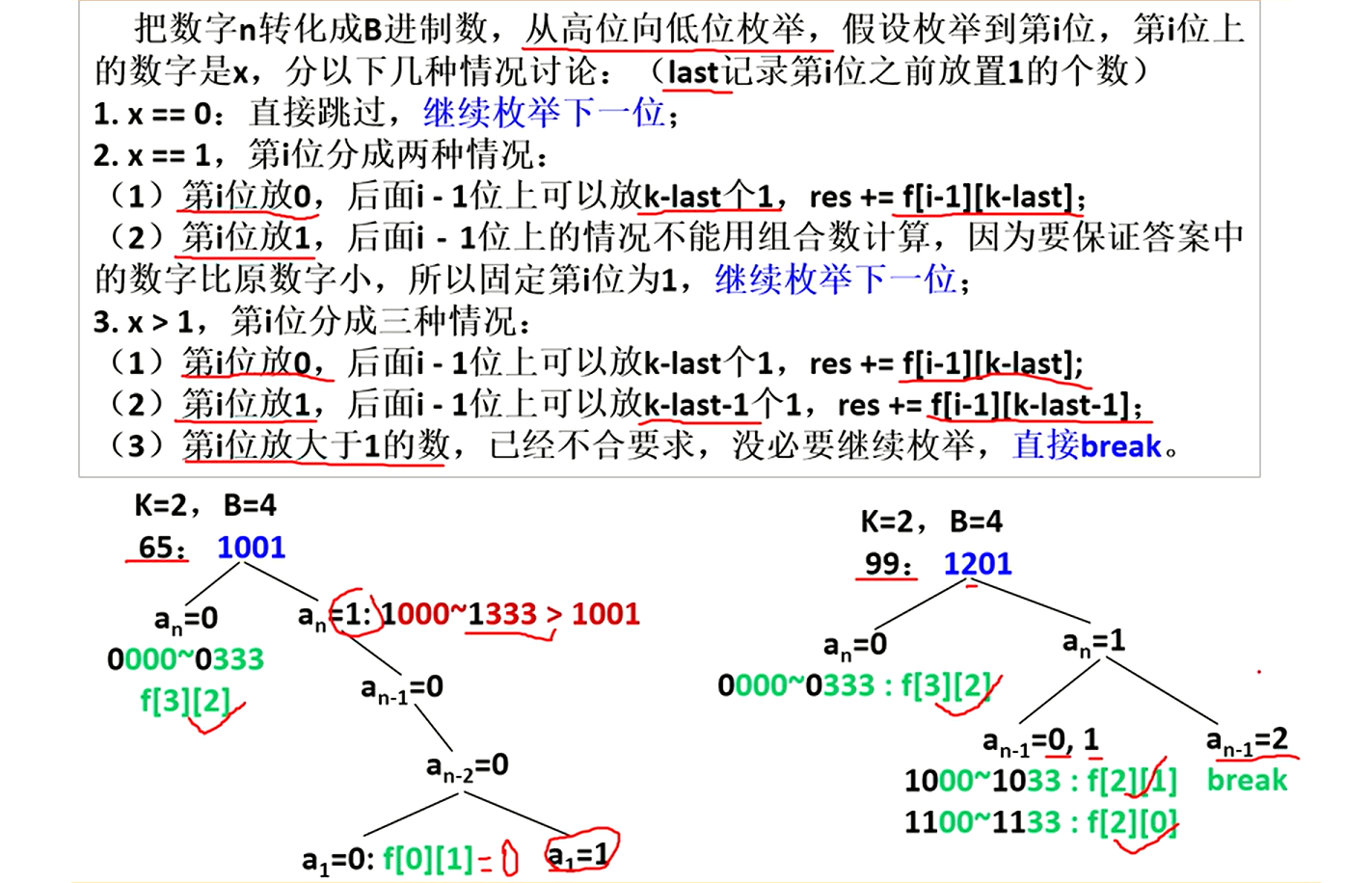
可以将题意转换为在一个区间$[x,y]$内，有多少个符合题意的数，这里的符合题意是指：这个数的B进制表示中，其中有K位上是1、其他位上全是0。

例如：

状态表示：f[i][j]表示在i个位置上，放置j个1的组合数

组合数的计算公式:$C_i^j=C_{i-1}^{j-1}+C_{i-1}^j$

可以理解为从i个数里面选j个数：对于第一个数：

• 选，再从i-1个里面选j-1个，$C_{i-1}^{j-1}$
• 不选，再从i-1个里面选j个，$C_{i-1}^j$

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 34;
int a[N];     //把B进制数的每一位抠出存入数组
int f[N][N];  //f[i][j]表示在i个位置上，放置j个1的组合数
int k, b;

void init() {
    for (int i = 0; i < N; i++) f[i][0] = 1;
    for (int i = 1; i < N; i++) {
        for (int j = 0; j <= i; j++) {
            f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
        }
    }
}

int dp(int n) {
    if (!n) return 0;
    int cnt = 0;
    while (n) a[++cnt] = n % b, n /= b;

    int res = 0, last = 0;   //last表示第i位之前放置1的个数
    for (int i = cnt; i >= 1; i--) {//从高位到低位枚举
        int now = a[i]; //当前的数字
        if (now >= 1) { //第i位==0时，直接跳过，继续枚举下一位
            res += f[i - 1][k - last]; //这一位放0
            if (now == 1) {  //第i位==1时，不能用组合数计算，继续枚举下一位    
                last++;
                if (last > k) break;
            } else {
                if (k - last - 1 >= 0) res += f[i - 1][k - last - 1];
                break; //第i位放大于1的数，不合要求，则break
            }
        }
        if (i == 1 && last == k) res++;//特判，走到末位的情况
    }
    return res;

}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    init();
    int l, r;
    cin >> l >> r >> k >> b;
    cout << dp(r) - dp(l - 1) << endl;
    return 0;
}