背包问题题目练习2

机器分配

题目

链接：https://www.acwing.com/problem/content/1015/

总公司拥有 $M$ 台相同的高效设备，准备分给下属的 $N$ 个分公司。

各分公司若获得这些设备，可以为国家提供一定的盈利。盈利与分配的设备数量有关。

问：如何分配这M台设备才能使国家得到的盈利最大？

求出最大盈利值。

分配原则：每个公司有权获得任意数目的设备，但总台数不超过设备数 $M$ 。

输入格式

第一行有两个数，第一个数是分公司数 $N$ ，第二个数是设备台数 $M$ ；

接下来是一个 $N \times M$ 的矩阵，矩阵中的第 $i$ 行第 $j$ 列的整数表示第 $i$ 个公司分配 $j$ 台机器时的盈利。

输出格式

第一行输出最大盈利值；

接下 $N$ 行，每行有 $2$ 个数，即分公司编号和该分公司获得设备台数。

答案不唯一，输出任意合法方案即可。

数据范围

$1 \le N \le 10$ ,
$1 \le M \le 15$

输入样例：

输出样例：

题目

将本题转换为分组背包问题：

分组背包问题：

有 $N$ 组物品和一个容量是 $V$ 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 $v_{ij}$ ，价值是 $w_{ij}$ ，其中 $i$ 是组号， $j$ 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

思路：

状态表示：f[i][j]表示前i组物品，能放入容量为j的背包的最大价值

循环物品组，循环背包容量，对于第i组物品，容量为j的背包，有s+1种选法，取最大值

将每家公司看成一个物品组，
分给第i个公司的不同机器数量可以分别看成一个物品组内的物品，即要么选0台，1台，，，m台，一定是这些选法里面的一种

动态规划：

状态表示：f[i][j]表示考虑前i个物品组，选法的总体积不超过j的方案的收益最大值
状态计算：集合划分：考虑前i个公司给多少个机器
- 不选或者选不了：f[i-1][j]
- 选第i个物品：f[i-1][j-k]+w[i][k]

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

int n, m;
int w[20][20];
int f[20][20]; //从前i个物品中选，总体积不超过j的方案的最大值
int path[20];

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> w[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            f[i][j] = f[i - 1][j];//不选;
            for (int k = 1; k <= j; k++) {//组内选多少个
                f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
            }
        }
    }
    cout << f[n][m] << endl;
    int j = m;
    for (int i = n; i >= 1; i--) {
        for (int k = 0; k <= j; k++) {
            if (f[i][j] == f[i - 1][j - k] + w[i][k]) {
                path[i] = k;
                j -= k;
                break;
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        cout << i << ' ' << path[i] << endl;
    }
    return 0;
}

金明的预算方案

题目

链接：https://www.acwing.com/problem/content/489/

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。

更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。

今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

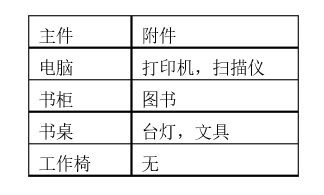
QQ截图20190313024710.png

如果要买归类为附件的物品，必须先买该附件所属的主件。

每个主件可以有0个、1个或2个附件。

附件不再有从属于自己的附件。

金明想买的东西很多，肯定会超过妈妈限定的N元。

于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。

他还从因特网上查到了每件物品的价格（都是10元的整数倍）。

他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为 $j_1，j_2，…，j_k$ ，则所求的总和为：

$v[j_1] * w[j_1]+v[j_2] * w[j_2]+…+v[j_k] * w[j_k]$ （其中*为乘号）

请你帮助金明设计一个满足要求的购物单。

输入格式

输入文件的第1行，为两个正整数，用一个空格隔开：N m，其中N表示总钱数，m为希望购买物品的个数。

从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有3个非负整数v p q，其中v表示该物品的价格，p表示该物品的重要度（1~5），q表示该物品是主件还是附件。

如果q=0，表示该物品为主件，如果q>0，表示该物品为附件，q是所属主件的编号。

输出格式

输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值 $（<200000）$ 。

数据范围

$N < 32000, m < 60, v < 10000$ $N < 32000, m < 60, v < 10000$

输入样例：

输出样例：

题目

可以将本题转换为分组背包问题：

主物品：代表多少组

附件：划分一个组中多少个物品

例如 2个附件 a1,a2,一个主物品c

可以组成： c | c,a1 | c,a2 | c,a1,a2

每个组中的划分只能用其中的一个

求出对应组的每个划分块需要多少钱（体积），钱*重要程度（相当于价值）

可以使用二进制枚举的方式，来计算附件选哪几件：

for (int k = 0; k < 1 << cxk.size(); k++) {
    int v = master[i].first, w = master[i].second; //体积，价值
    for (int u = 0; u < cxk.size(); u++) {
        if (k >> u & 1) { //1代表选
            v += cxk[u].first;
            w += cxk[u].second;
        }
    }
    if (j >= v) {
        f[j] = max(f[j], f[j - v] + w);
    }
}

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;
typedef pair<int, int> PII;

vector<PII> master(100);
vector<PII> servent[100];
int f[32010];
int n, m;


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> m >> n;
    for (int i = 1; i <= n; i++) {
        int v, p, q;
        cin >> v >> p >> q;
        if (q == 0) master[i] = {v, v * p};
        else servent[q].push_back({v, v * p});
    }

    for (int i = 1; i <= n; i++) {
        if (master[i].first) { //是主件
            for (int j = m; j >= 0; j--) {
                vector<PII> cxk = servent[i]; //所有附件
                for (int k = 0; k < 1 << cxk.size(); k++) {
                    int v = master[i].first, w = master[i].second; //体积，价值
                    for (int u = 0; u < cxk.size(); u++) {
                        if (k >> u & 1) {
                            v += cxk[u].first;
                            w += cxk[u].second;
                        }
                    }
                    if (j >= v) {
                        f[j] = max(f[j], f[j - v] + w);
                    }
                }
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

开心的金明

题目：

链接：https://www.acwing.com/problem/content/428/

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间他自己专用的很宽敞的房间。

更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 $N$ 元钱就行”。

今天一早金明就开始做预算，但是他想买的东西太多了，肯定会超过妈妈限定的 $N$ 元。

于是，他把每件物品规定了一个重要度，分为 $5$ 等：用整数 $1 \sim 5$ 表示，第 $5$ 等最重要。

他还从因特网上查到了每件物品的价格（都是整数元）。

他希望在不超过 $N$ 元（可以等于 $N$ 元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 $j$ 件物品的价格为 $v[j]$ ，重要度为 $w[j]$ ，共选中了 $k$ 件物品，编号依次为 $j_1，j_2，…，j_k$ ，则所求的总和为：

v[j_1] \times w[j_1]+v[j_2] \times w[j_2]+…+v[j_k] \times w[j_k]

请你帮助金明设计一个满足要求的购物单。

输入格式

输入文件的第 $1$ 行，为两个正整数 $N$ 和 $m$ ，用一个空格隔开。（其中 $N$ 表示总钱数， $m$ 为希望购买物品的个数）

从第 $2$$2$ 行到第 $m+1$ 行，第 $j$ 行给出了编号为 $j-1$ 的物品的基本数据，每行有 $2$ 个非负整数 $v$ 和 $p$ 。（其中 $v$ 表示该物品的价格， $p$ 表示该物品的重要度）

输出格式

输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（数据保证结果不超过 $10^8$ ）。

数据范围

$1 \le N < 30000$ ,
$1 \le m < 25$ ,
$0 \le v \le 10000$ ,
$1 \le p \le 5$

输入样例：

输出样例：

题目

01背包问题：

状态计算：f[i][j]表示所有从前i个物品选，且总体积不超过j的选法集合中的价值最大值

集合划分：

按照第i种物品选或者不选划分 f[i][j]集合。
不选第i种物品,f[i][j] = f[i-1][j];
- 问题转化为从前i-1个物品选，且总体积不超过j的选法集合中的最大值。
选第i种物品, f[i][j] = f[i-1][j-v] + v*w ;
- 已经确定选第i种物品，那么问题转化为从前i-1个物品选，且总体积不超过j-v的选法集合中的最大值再加上 v*w。

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int n, m;
    cin >> m >> n;
    vector<int> f(m + 1);
    for (int i = 1; i <= n; i++) {
        int a, b;
        cin >> a >> b;
        int v = a, w = b * a;
        for(int j=m;j>=v;j--)
            f[j]= max(f[j],f[j-v]+w);
    }
    cout<<f[m]<<endl;     
  	return 0;
}

货币系统

题目

链接：https://www.acwing.com/problem/content/1023/

给你一个n种面值的货币系统，求组成面值为m的货币有多少种方案。

输入格式

第一行，包含两个整数n和m。

接下来n行，每行包含一个整数，表示一种货币的面值。

输出格式

共一行，包含一个整数，表示方案数。

数据范围

$n≤15,m≤3000$

输入样例：

输出样例：

题目

这是一个完全背包求方案数的模版

完全背包问题：

动态规划：

状态表示：f[i,j]表示所有从前i个物品中选，且总体积恰好是j的方案

状态计算：

f[i,j] = f[i-1,j]+f[i-1,j-v*1]+f[i-1.j-v*2]+...+f[i-1,j-v*s]
f[i,j-v]= f[i-1,j-v*1]+f[i-1,j-v*2]+...+f[i-1,j-v*s]

可以得出：f[i,j]=f[i-1,j]+f[i,j-v]

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int n, m;
    cin >> n >> m;
    vector<int> f(m + 1);
    f[0] = 1;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> x;
        for (int j = x; j <= m; j++) {
            f[j] += f[j - x];
        }
    }
    cout<<f[m]<<endl;

    return 0;
}

货币系统2

题目

链接：https://www.acwing.com/problem/content/534/

在网友的国度中共有 $n$ 种不同面额的货币，第 $i$ 种货币的面额为 $a[i]$ ，你可以假设每一种货币都有无穷多张。

为了方便，我们把货币种数为 $n$$n$ 、面额数组为 $a[1..n]$ 的货币系统记作 $(n,a)$ 。

在一个完善的货币系统中，每一个非负整数的金额 $x$ 都应该可以被表示出，即对每一个非负整数 $x$ ，都存在 $n$ 个非负整数 $t[i]$ 满足 $a[i] × t[i]$ 的和为 $x$ 。

然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额 $x$ 不能被该货币系统表示出。

例如在货币系统 $n=3, a=[2,5,9]$ 中，金额 $1,3$ 就无法被表示出来。

两个货币系统 $(n,a)$ 和 $(m,b)$ 是等价的，当且仅当对于任意非负整数 $x$ ，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。

他们希望找到一个货币系统 $(m,b)$ ，满足 $(m,b)$ 与原来的货币系统 $(n,a)$ 等价，且 $m$ 尽可能的小。

他们希望你来协助完成这个艰巨的任务：找到最小的 $m$ 。

输入格式

输入文件的第一行包含一个整数 $T$ ，表示数据的组数。

接下来按照如下格式分别给出 $T$ 组数据。

每组数据的第一行包含一个正整数 $n$ 。

接下来一行包含 $n$ 个由空格隔开的正整数 $a[i]$ 。

输出格式

输出文件共有 $T$ 行，对于每组数据，输出一行一个正整数，表示所有与 $(n,a)$ 等价的货币系统 $(m,b)$ 中，最小的 $m$ 。

数据范围

$1 \le n \le 100$ ,
$1 \le a[i] \le 25000$ ,
$1 \le T \le 20$

输入样例：



19 10 6 

29 13 19 17 

输出样例：

2
5

题目

完全背包问题：求极大无关向量组的个数我们会发现，所有能被其他货币表示出来的货币都可以被删除，那么这样就可以直接做了，直接把能被其他表示出来的去除即可。

可以先将这个序列排序，然后从小的数开始去晒掉大的数。

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) cin >> a[i];
    std::sort(a.begin() + 1, a.end());
    vector<int> f(a[n] + 1);
    f[0] = 1; //当前体积为j的所有方案。
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        if (f[a[i]]) continue;
        ans++;
        for (int j = a[i]; j <= a[n]; j++) {
            f[j] |= f[j - a[i]];
        }
    }
    cout << ans << endl;
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int _;
    cin >> _;
    while (_--) solve();
    return 0;
}

能量石

题目

链接：https://www.acwing.com/problem/content/736/

岩石怪物杜达生活在魔法森林中，他在午餐时收集了 $N$ 块能量石准备开吃。

由于他的嘴很小，所以一次只能吃一块能量石。

能量石很硬，吃完需要花不少时间。

吃完第 $i$ 块能量石需要花费的时间为 $S_i$ 秒。

杜达靠吃能量石来获取能量。

不同的能量石包含的能量可能不同。

此外，能量石会随着时间流逝逐渐失去能量。

第 $i$ 块能量石最初包含 $E_i$ 单位的能量，并且每秒将失去 $L_i$ 单位的能量。

当杜达开始吃一块能量石时，他就会立即获得该能量石所含的全部能量（无论实际吃完该石头需要多少时间）。

能量石中包含的能量最多降低至 $0$ 。

请问杜达通过吃能量石可以获得的最大能量是多少？

输入格式

第一行包含整数 $T$ ，表示共有 $T$ 组测试数据。

每组数据第一行包含整数 $N$ ，表示能量石的数量。

接下来 $N$ 行，每行包含三个整数 $S_i,E_i,L_i$ 。

输出格式

每组数据输出一个结果，每个结果占一行。

结果表示为 Case #x: y，其中 $x$ 是组别编号（从 $1$ 开始）， $y$ 是可以获得的最大能量值。

数据范围

$1 \le T \le 10$ ,
$1 \le N \le 100$ ,
$1 \le S_i \le 100$ ,
$1 \le E_i \le 10^5$ ,
$0 \le L_i \le 10^5$

输入样例：

输出样例：

Case #1: 105
Case #2: 8
Case #3: 500

样例解释

在样例＃1中，有 $N = 4$ 个宝石。杜达可以选择的一个吃石头顺序是：

吃第四块石头。这需要 $5$ 秒，并给他 $80$ 单位的能量。
吃第二块石头。这需要 $5$ 秒，并给他 $5$ 单位的能量（第二块石头开始时具有 $30$ 单位能量， $5$ 秒后失去了 $25$ 单位的能量）。
吃第三块石头。这需要 $100$ 秒，并给他 $20$ 单位的能量（第三块石头开始时具有 $30$ 单位能量， $10$ 秒后失去了 $10$ 单位的能量）。
吃第一块石头。这需要 $20$ 秒，并给他 $0$ 单位的能量（第一块石头以 $10$ 单位能量开始， $110$ 秒后已经失去了所有的能量）。

他一共获得了 $105$ 单位的能量，这是能获得的最大值，所以答案是 $105$ 。

在样本案例＃2中，有 $N = 3$ 个宝石。

无论杜达选择吃哪块石头，剩下的两个石头的能量都会耗光。

所以他应该吃第三块石头，给他提供 $8$ 单位的能量。

在样本案例＃3中，有 $N = 2$ 个宝石。杜达可以：

吃第一块石头。这需要 $12$ 秒，并给他 $300$ 单位的能量。
吃第二块石头。这需要 $5$ 秒，并给他 $200$ 单位的能量（第二块石头随着时间的推移不会失去任何能量！）。

所以答案是 $500$ 。

题目

对于两个能量石 $i,j$ 来说，如果他们交换之后对答案的贡献不增加，那么应该满足：

$e_i+e_j-s_i*l_j>=e_j+e_i-s_j*l_i$

化简得：

$s_j*l_i>=s_i*l_j$

因此我们可以按照这个顺序对所有的能量石进行排序，贪心的拿最优的方案。

每个能量石都是拿与不拿的选择，那么这就是一个01背包问题了：

状态表示：f[i,j]表示所有只从前i块能量石中选，且总体积不超过j的方案的最大值

状态计算：f[i,j]=max(f[i-1,j],f[i-1,j-s]+e-(j-s)*L)

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

typedef struct node {
    int s, e, l;
    bool operator<(const node cxk) const {
        return s * cxk.l < cxk.s * l;
    }
} node;

int solve() {
    int n;
    cin >> n;
    vector<node> a(n + 1);
    int m = 0;
    for (int i = 1; i <= n; i++) {
        int s, e, l;
        cin >> s >> e >> l;
        a[i] = {s, e, l};
        m += s;
    }
    std::sort(a.begin() + 1, a.end());
    vector<int> f(m + 1, -0x3f3f3f3f);
    f[0] = 0;
    for (int i = 1; i <= n; i++) {
        int s = a[i].s, e = a[i].e, l = a[i].l;
        for (int j = m; j >= s; j--) {
            f[j] = max(f[j], f[j - s] + e - (j - s) * l);
        }
    }
    int res=0;
    for(int i=0;i<=m;i++) res= max(res,f[i]);
    return res;
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int t;
    cin >> t;
    for (int i = 1; i <= t; i++) {
        std::printf("Case #%d: %d\n",i, solve());
    }
    return 0;
}

机器分配​

题目​

输入格式​

输出格式​

数据范围​

输入样例：​

输出样例：​

题目​

代码​

金明的预算方案​

题目​

输入格式​

输出格式​

数据范围​

输入样例：​

输出样例：​

题目​

代码​

开心的金明​

题目：​

输入格式​

输出格式​

数据范围​

输入样例：​

输出样例：​

题目​

代码​

货币系统​

题目​

输入格式​

输出格式​

数据范围​

输入样例：​

输出样例：​

题目​

代码​

货币系统2​

题目​

输入格式​

输出格式​

数据范围​

输入样例：​

输出样例：​

题目​

代码​

能量石​

题目​

输入格式​

输出格式​

数据范围​

输入样例：​

输出样例：​

样例解释​

题目​

代码​

机器分配

题目

输入格式

输出格式

数据范围

输入样例：

输出样例：

题目

代码

金明的预算方案

题目

输入格式

输出格式

数据范围

输入样例：

输出样例：

题目

代码

开心的金明

题目：

输入格式

输出格式

数据范围

输入样例：

输出样例：

题目

代码

货币系统

题目

输入格式

输出格式

数据范围

输入样例：

输出样例：

题目

代码

货币系统2

题目

输入格式

输出格式

数据范围

输入样例：

输出样例：

题目

代码

能量石

题目

输入格式

输出格式

数据范围

输入样例：

输出样例：

样例解释

题目

代码