概率DP求期望

[NOIP2016 提高组] 换教室

链接：https://www.luogu.com.cn/problem/P1850

题目描述

对于刚上大学的牛牛来说，他面临的第一个问题是如何根据实际情况申请合适的课程。

在可以选择的课程中，有 $2n$ 节课程安排在 $n$ 个时间段上。在第 $i$ （ $1 \leq i \leq n$ ）个时间段上，两节内容相同的课程同时在不同的地点进行，其中，牛牛预先被安排在教室 $c_i$ 上课，而另一节课程在教室 $d_i$ 进行。

在不提交任何申请的情况下，学生们需要按时间段的顺序依次完成所有的 $n$ 节安排好的课程。如果学生想更换第 $i$ 节课程的教室，则需要提出申请。若申请通过，学生就可以在第 $i$ 个时间段去教室 $d_i$ 上课，否则仍然在教室 $c_i$ 上课。

由于更换教室的需求太多，申请不一定能获得通过。通过计算，牛牛发现申请更换第 $i$ 节课程的教室时，申请被通过的概率是一个已知的实数 $k_i$ ，并且对于不同课程的申请，被通过的概率是互相独立的。

学校规定，所有的申请只能在学期开始前一次性提交，并且每个人只能选择至多 $m$ 节课程进行申请。这意味着牛牛必须一次性决定是否申请更换每节课的教室，而不能根据某些课程的申请结果来决定其他课程是否申请；牛牛可以申请自己最希望更换教室的 $m$ 门课程，也可以不用完这 $m$ 个申请的机会，甚至可以一门课程都不申请。

因为不同的课程可能会被安排在不同的教室进行，所以牛牛需要利用课间时间从一间教室赶到另一间教室。

牛牛所在的大学有 $v$ 个教室，有 $e$ 条道路。每条道路连接两间教室，并且是可以双向通行的。由于道路的长度和拥堵程度不同，通过不同的道路耗费的体力可能会有所不同。当第 $i$ （ $1 \leq i \leq n-1$ ）节课结束后，牛牛就会从这节课的教室出发，选择一条耗费体力最少的路径前往下一节课的教室。

现在牛牛想知道，申请哪几门课程可以使他因在教室间移动耗费的体力值的总和的期望值最小，请你帮他求出这个最小值。

输入格式

第一行四个整数 $n,m,v,e$ 。 $n$ 表示这个学期内的时间段的数量； $m$ 表示牛牛最多可以申请更换多少节课程的教室； $v$ 表示牛牛学校里教室的数量； $e$ 表示牛牛的学校里道路的数量。

第二行 $n$ 个正整数，第 $i$ （ $1 \leq i \leq n$ ）个正整数表示 $c_i$ ，即第 $i$ 个时间段牛牛被安排上课的教室；保证 $1 \le c_i \le v$ 。

第三行 $n$ 个正整数，第 $i$ （ $1 \leq i \leq n$ ）个正整数表示 $d_i$ ，即第 $i$ 个时间段另一间上同样课程的教室；保证 $1 \le d_i \le v$ 。

第四行 $n$ 个实数，第 $i$ （ $1 \leq i \leq n$ ）个实数表示 $k_i$ ，即牛牛申请在第 $i$ 个时间段更换教室获得通过的概率。保证 $0 \le k_i \le 1$ 。

接下来 $e$ 行，每行三个正整数 $a_j, b_j, w_j$ ，表示有一条双向道路连接教室 $a_j, b_j$ ，通过这条道路需要耗费的体力值是 $w_j$ ；保证 $1 \le a_j, b_j \le v$ ， $1 \le w_j \le 100$ 。

保证 $1 \leq n \leq 2000$ ， $0 \leq m \leq 2000$ ， $1 \leq v \leq 300$ ， $0 \leq e \leq 90000$ 。

保证通过学校里的道路，从任何一间教室出发，都能到达其他所有的教室。

保证输入的实数最多包含 $3$ 位小数。

输出格式

输出一行，包含一个实数，四舍五入精确到小数点后恰好 $2$ 位，表示答案。你的输出必须和标准输出完全一样才算正确。

测试数据保证四舍五入后的答案和准确答案的差的绝对值不大于 $4 \times 10^{-3}$ 。（如果你不知道什么是浮点误差，这段话可以理解为：对于大多数的算法，你可以正常地使用浮点数类型而不用对它进行特殊的处理）

样例输入 #1

样例输出 #1

2.80

【样例1说明】

所有可行的申请方案和期望收益如下表:

【提示】

道路中可能会有多条双向道路连接相同的两间教室。也有可能有道路两端连接的是同一间教室。
请注意区分n,m,v,e的意义, n不是教室的数量, m不是道路的数量。

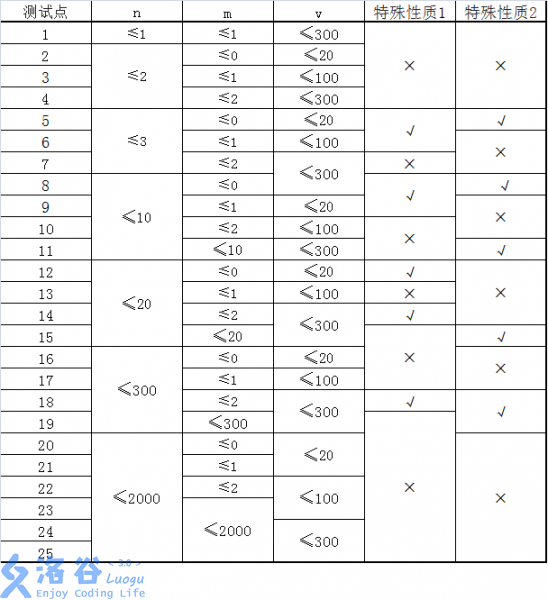
特殊性质1:图上任意两点 $a_i$ , $b_i$ , $a_i$ ≠ $b_i$ 间,存在一条耗费体力最少的路径只包含一条道路。

特殊性质2:对于所有的 $1≤ i≤ n$ ， $k_i= 1$ 。

题目

概率dp求期望:

状态表示：f[i][j][0/1]表示当前为第i个时段，已经用了j次换教室的机会，这次换/不换的路径总和的最小期望

初始化：f[1][0][0]=f[1][1][1]=0,其他正无

答案为：min(f[n][i][0/1]), $i \in [0,m]$

状态转移：

上次不换，这次不换：f[i - 1][j][0] + dist[c[i - 1]][c[i]];
上次换，这次不换：f[i - 1][j][1] + dist[c[i - 1]][c[i]] * (1 - p[i - 1]) + dist[d[i - 1]][c[i]] * p[i - 1];
上次不换，这次换：f[i - 1][j - 1][0] + dist[c[i - 1]][c[i]] * (1 - p[i]) + dist[c[i - 1]][d[i]] * p[i];
上次换，这次换：
- 分上次成功，这次成功，
- 上次成功，这次失败
- 上次失败，这次成功，
- 上次失败，这次失败

double t4 = f[i - 1][j - 1][1];
t4 += dist[c[i - 1]][c[i]] * (1 - p[i - 1]) * (1 - p[i]);
t4 += dist[c[i - 1]][d[i]] * (1 - p[i - 1]) * p[i];
t4 += dist[d[i - 1]][c[i]] * p[i - 1] * (1 - p[i]);
t4 += dist[d[i - 1]][d[i]] * p[i - 1] * p[i];

教室与教室之间的路径可以使用floyd算法求解。

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 2010;
int n, m, v, e;
int c[N], d[N];
double p[N], f[N][N][2], dist[N][N];

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n >> m >> v >> e;
    for (int i = 1; i <= n; i++) cin >> c[i];
    for (int i = 1; i <= n; i++) cin >> d[i];
    for (int i = 1; i <= n; i++) cin >> p[i];

    for (int i = 1; i <= v; i++) {
        for (int j = 1; j <= v; j++) {
            if (i != j) dist[i][j] = 1e18;
        }
    }

    for (int i = 1; i <= e; i++) {
        int x, y, w;
        cin >> x >> y >> w;
        dist[x][y] = dist[y][x] = min(dist[x][y], 1.0 * w);
    }

    for (int k = 1; k <= v; k++) {
        for (int i = 1; i <= v; i++) {
            for (int j = 1; j <= v; j++) {
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
            }
        }
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            f[i][j][0] = f[i][j][1] = 1e18;
        }
    }
    f[1][0][0] = f[1][1][1] = 0;


    for (int i = 2; i <= n; i++) {
        for (int j = 0; j <= min(i, m); j++) {
            //上次不换，这次不换
            double t1 = f[i - 1][j][0] + dist[c[i - 1]][c[i]];
            //上次换，这次不换
            double t2 = f[i - 1][j][1] + dist[c[i - 1]][c[i]] * (1 - p[i - 1]) + dist[d[i - 1]][c[i]] * p[i - 1];
            f[i][j][0] = min(t1, t2);
            //上次不换，这次换
            if (j == 0) continue;
            double t3 = f[i - 1][j - 1][0] + dist[c[i - 1]][c[i]] * (1 - p[i]) + dist[c[i - 1]][d[i]] * p[i];
            //上次换，这次换
            double t4 = f[i - 1][j - 1][1];
            t4 += dist[c[i - 1]][c[i]] * (1 - p[i - 1]) * (1 - p[i]);
            t4 += dist[c[i - 1]][d[i]] * (1 - p[i - 1]) * p[i];
            t4 += dist[d[i - 1]][c[i]] * p[i - 1] * (1 - p[i]);
            t4 += dist[d[i - 1]][d[i]] * p[i - 1] * p[i];
            f[i][j][1] = min(t3, t4);
        }
    }
    double res = 1e18;
    for (int j = 0; j <= m; j++) {
        res = min(res, min(f[n][j][0], f[n][j][1]));
    }
    std::printf("%.2f", res);


    return 0;
}

绿豆蛙的归宿

题目背景

随着新版百度空间的上线，Blog 宠物绿豆蛙完成了它的使命，去寻找它新的归宿。

题目描述

给出张 $n$ 个点 $m$ 条边的有向无环图，起点为 $1$ ，终点为 $n$ ，每条边都有一个长度，并且从起点出发能够到达所有的点，所有的点也都能够到达终点。

绿豆蛙从起点出发，走向终点。到达每一个顶点时，如果该节点有 $k$ 条出边，绿豆蛙可以选择任意一条边离开该点，并且走向每条边的概率为 $\frac{1}{k}$ 。现在绿豆蛙想知道，从起点走到终点的所经过的路径总长度期望是多少？

输入格式

输入的第一行是两个整数，分别代表图的点数 $n$ 和边数 $m$ 。

第 $2$ 到第 $(m + 1)$ 行，每行有三个整数 $u, v, w$ ，代表存在一条从 $u$ 指向 $v$ 长度为 $w$ 的有向边。

输出格式

输出一行一个实数代表答案，四舍五入保留两位小数。

样例输入 #1

样例输出 #1

7.00

数据规模与约定

对于 $20\%$ 的数据，保证 $n \leq 10^2$ 。
对于 $40\%$ 的数据，保证 $n \leq 10^3$ 。
对于 $60\%$ 的数据，保证 $n \leq 10^4$ 。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 10^5$ ， $1 \leq m \leq 2 \times n$ ， $1 \leq u, v \leq n$ ， $1 \leq w \leq 10^9$ ，给出的图无重边和自环。

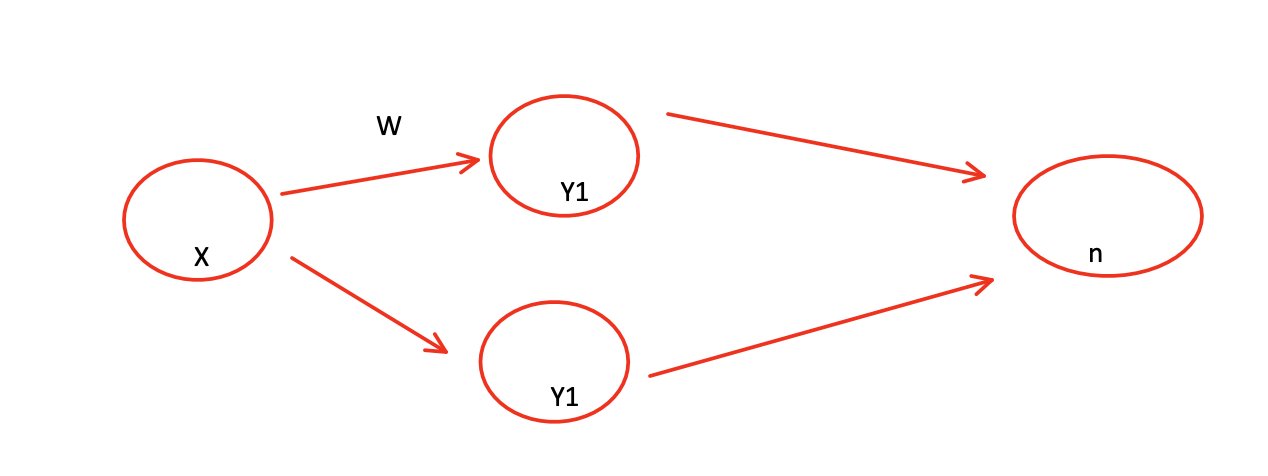
记忆化搜索

f[i]表示从i走到终点n的路径总长的期望

起点：f[n]=0

终点：f[1]

转移：f[x]+=(f[y]+w)*d[x]

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 1e5 + 10;
int n, m;
vector<pair<int, int>> e[N];
vector<int> d(N);
vector<double> f(N);//从i走到u的期望

double dfs(int x) {
    if (f[x]) return f[x];
    for (auto [y, w]: e[x]) {
        f[y] = dfs(y);
        f[x] += (f[y] + w) * 1.0 / d[x];
    }
    return f[x];
}


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].emplace_back(b, c);
        d[a]++;
    }
    dfs(1);
    std::printf("%.2f", f[1]);
    return 0;
}

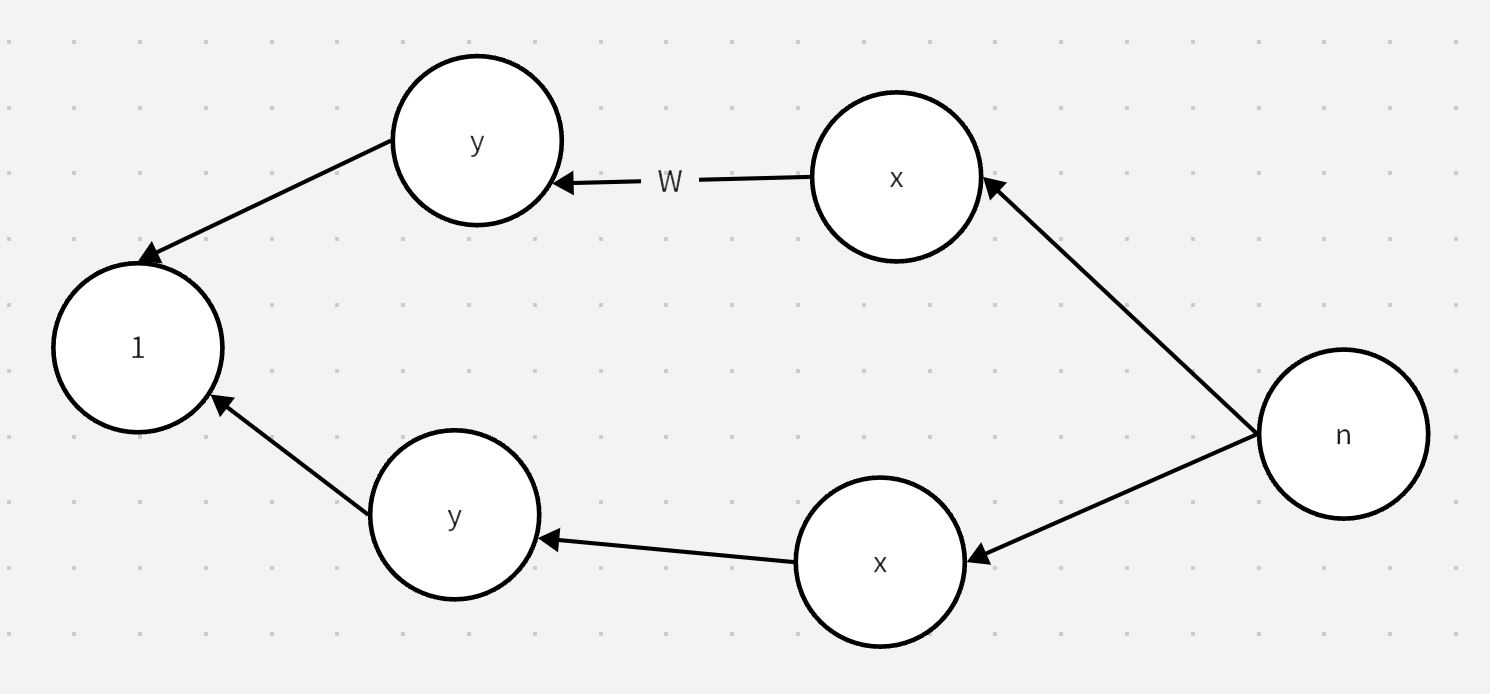
拓扑排序

需要反向建图

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 1e5 + 10;
typedef pair<int, int> PII;
vector<PII> e[N];
int n, m;
vector<int> d(N), k(N);
vector<double> f(N);

void topsort() {
    queue<int> q;
    q.push(n);
    while (q.size()) {
        auto x = q.front();
        q.pop();
        for (auto [y, w]: e[x]) {
            f[y] += (f[x] + w) * 1 / k[y];
            if (--d[y] == 0)q.push(y);
        }
    }
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        e[b].push_back({a, c});
        d[a]++, k[a]++;
    }
    topsort();
    std::printf("%.2f", f[1]);


    return 0;
}

[NOIP2016 提高组] 换教室​

题目描述​

输入格式​

输出格式​

样例输入 #1​

样例输出 #1​

题目​

代码​

绿豆蛙的归宿​

题目背景​

题目描述​

输入格式​

输出格式​

样例输入 #1​

样例输出 #1​

数据规模与约定​

记忆化搜索​

代码​

拓扑排序​

代码​

[NOIP2016 提高组] 换教室

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

题目

代码

绿豆蛙的归宿

题目背景

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

数据规模与约定

记忆化搜索

代码

拓扑排序

代码