SCCTarjan算法

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。 下图中，子图4为一个强连通分量，因为顶点1,2,3,4两两可达。5,6也分别是两个强连通分量。

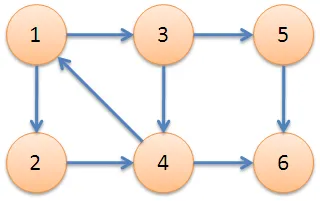
DFS生成树：

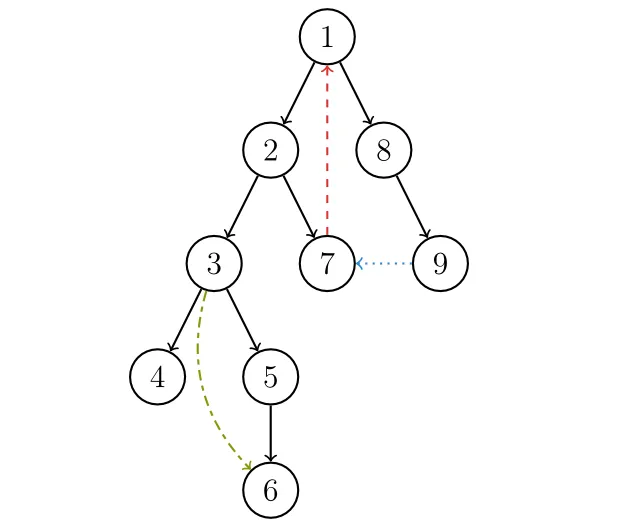
1. 树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边（back edge）：示意图中以红色边表示（即7->1 ），也被叫做回边，即指向祖先结点的边。
3. 横叉边（cross edge）：示意图中以蓝色边表示（即9->7 ），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
4. 前向边（forward edge）：示意图中以绿色边表示（即3->6 ），它是在搜索的时候遇到子树中的结点的时候形成的。

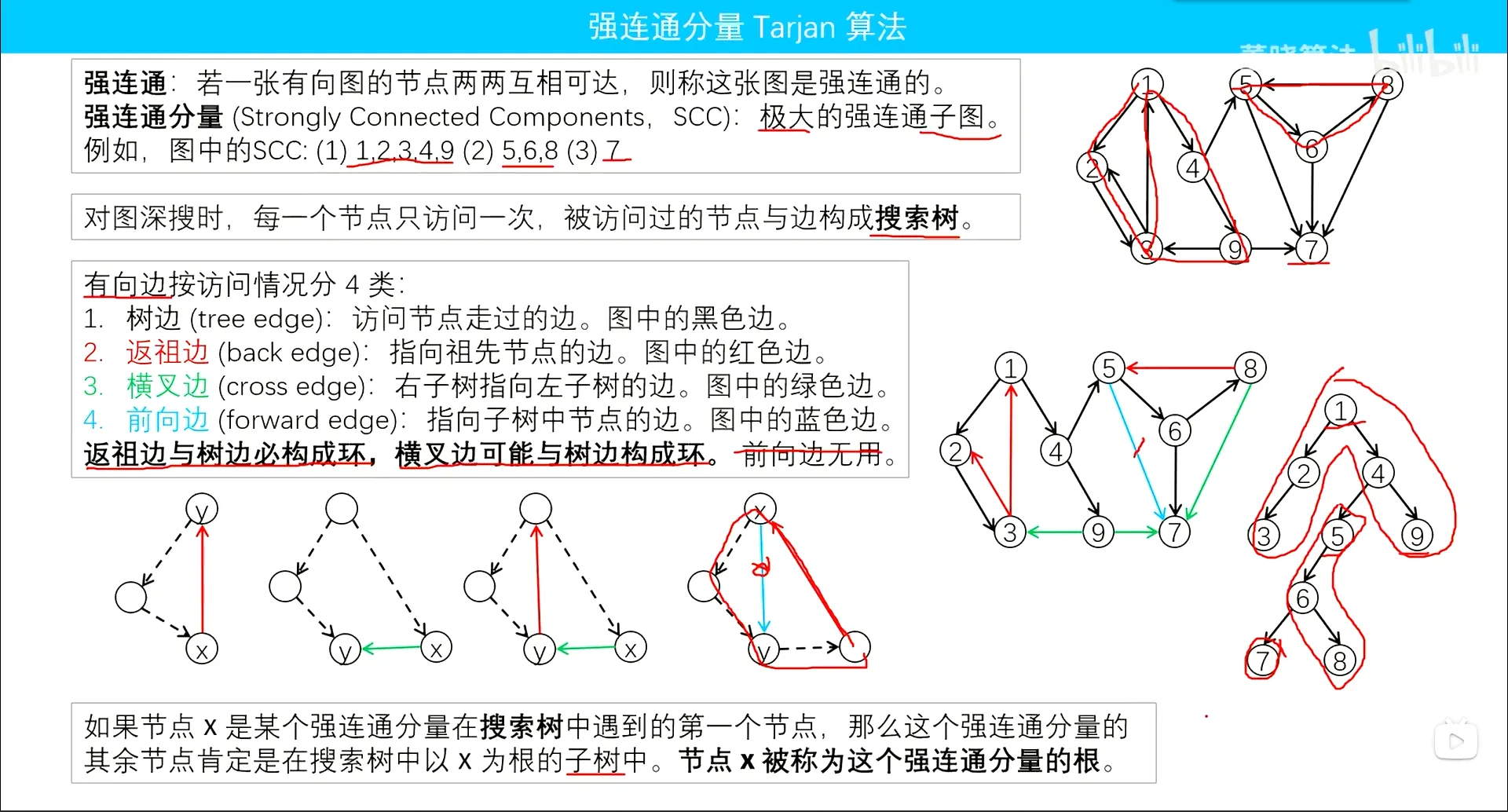
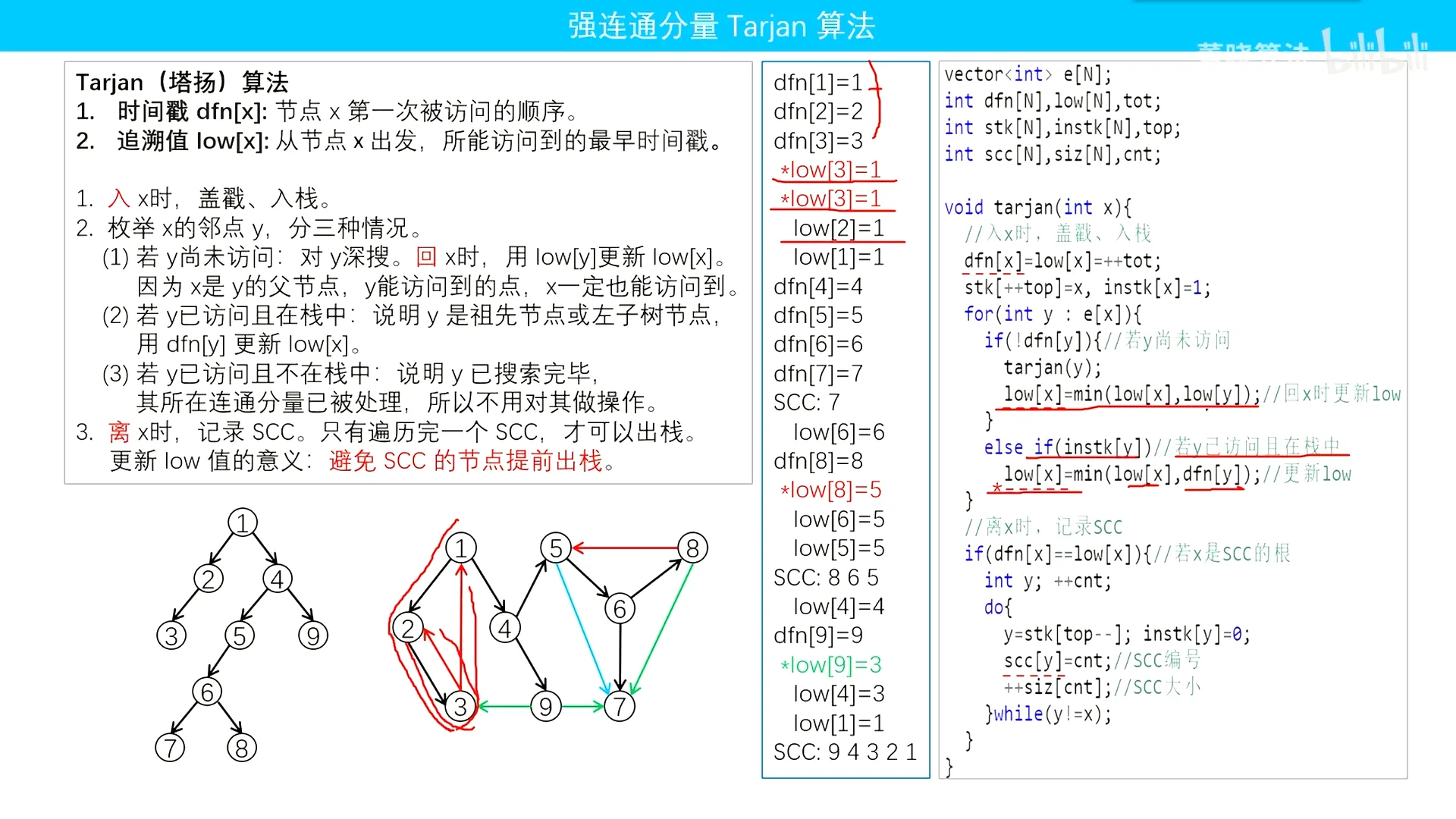
默写tarjan算法梳理的思路：

1. 加时间戳；
2. 放入栈中，做好标记；
3. 遍历邻点：
   1. 如果没遍历过，tarjan一遍，用low[j]更新最小值low；
   2. 如果在栈中，用dfn[j]更新最小值low
4. 找到最高点：
   1. scc个数++
   2. do-while循环：从栈中取出每个元素；标志为出栈；对元素做好属于哪个scc；该scc中点的数量+ +

vector<int> e[N]; 
int dfn[N],low[N],tot;
int stk[N],instk[N],top;
int scc[N],siz[N],cnt;

void tarjan(int x){
  //入x时，盖戳、入栈
  dfn[x]=low[x]=++tot;
  stk[++top]=x,instk[x]=1;
  for(int y : e[x]){
    if(!dfn[y]){//若y尚未访问
      tarjan(y);
      low[x]=min(low[x],low[y]);//回x时更新low
    }
    else if(instk[y])//若y已访问且在栈中
      low[x]=min(low[x],dfn[y]);//在x时更新low
  }
  //离x时，收集SCC
  if(dfn[x]==low[x]){//若x是SCC的根
    int y; ++cnt;
    do{
      y=stk[top--];
      instk[y]=0;
      scc[y]=cnt;//SCC编号
      ++siz[cnt];//SCC大小
    }while(y!=x);
  }
}