对顶堆

对顶堆可以动态维护一个序列上的第k大的数，由一个大根堆和一个小根堆组成，

• 小根堆维护前k大的数(包含第k个)
• 大根堆维护比第k个数小的数

[CSP-J2020] 直播获奖

题目描述

NOI2130 即将举行。为了增加观赏性，CCF 决定逐一评出每个选手的成绩，并直播即时的获奖分数线。本次竞赛的获奖率为 $w\%$，即当前排名前 $w\%$ 的选手的最低成绩就是即时的分数线。

更具体地，若当前已评出了 $p$ 个选手的成绩，则当前计划获奖人数为 $\max(1, \lfloor p \times w \%\rfloor)$，其中 $w$ 是获奖百分比，$\lfloor x \rfloor$ 表示对 $x$ 向下取整，$\max(x,y)$ 表示 $x$ 和 $y$ 中较大的数。如有选手成绩相同，则所有成绩并列的选手都能获奖，因此实际获奖人数可能比计划中多。

作为评测组的技术人员，请你帮 CCF 写一个直播程序。

输入格式

第一行有两个整数 $n, w$。分别代表选手总数与获奖率。
第二行有 $n$ 个整数，依次代表逐一评出的选手成绩。

输出格式

只有一行，包含 $n$ 个非负整数，依次代表选手成绩逐一评出后，即时的获奖分数线。相邻两个整数间用一个空格分隔。

样例输入 #1

10 60
200 300 400 500 600 600 0 300 200 100

样例输出 #1

200 300 400 400 400 500 400 400 300 300

样例输入 #2

10 30
100 100 600 100 100 100 100 100 100 100

样例输出 #2

100 100 600 600 600 600 100 100 100 100

提示

样例 1 解释

---

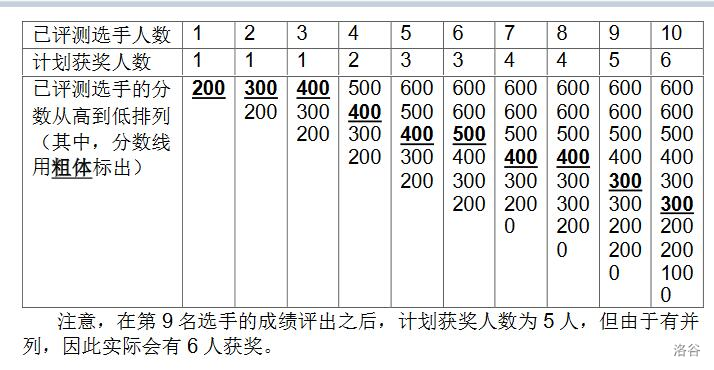
数据规模与约定

各测试点的 $n$ 如下表：

测试点编号	$n=$
$1 \sim 3$	$10$
$4 \sim 6$	$500$
$7 \sim 10$	$2000$
$11 \sim 17$	$10^4$
$18 \sim 20$	$10^5$

对于所有测试点，每个选手的成绩均为不超过 $600$ 的非负整数，获奖百分比 $w$ 是一个正整数且 $1 \le w \le 99$。

---

提示

在计算计划获奖人数时，如用浮点类型的变量（如 C/C++ 中的 float 、 double，Pascal 中的 real 、 double 、 extended 等）存储获奖比例 $w\%$，则计算 $5 \times 60\%$ 时的结果可能为 $3.000001$，也可能为 $2.999999$，向下取整后的结果不确定。因此，建议仅使用整型变量，以计算出准确值。

思路

模版题： k为i*w/100

• 使用一个大根堆x维护比第k个数小的数
• 使用一个小根堆y来维护前k大的数

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    int n, w;
    cin >> n >> w;
    priority_queue<int> x;//大根堆 ，维护 ai<q
    priority_queue<int, vector<int>, greater<>> y;//小根堆，维护ai>=q;
    for (int i = 1; i <= n; i++) {
        int a;
        cin >> a;
        if (y.empty() || a >= y.top()) y.push(a);
        else x.push(a);
        int k = max((int) 1, i * w / 100);
        while (y.size() > k) x.push(y.top()), y.pop();//保持小根堆有k个元素
        while (y.size() < k) y.push(x.top()), x.pop();
        cout << y.top() << " ";
    }
}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    while (_--) solve();
    return 0;
}

[ABC306E] Best Performances

题面翻译

题目描述：

给定长度为 $N$ 的数列 $A=(A_1,A_2,\dots,A_N)$，最开始所有项均为 $0$。

定义函数 $f(A)$ 如下：

将 $A$ 按照降序（即使得 $A$ 为广义单调递减序列）排序得到 $B$。 则 $f(A)=B_1+B_2+\dots+B_K$，其中 $B$ 为排序后的数列，$K$ 为 $A$ 中不为 $0$ 的元素个数。

现在对该数列进行 $Q$ 次更新。对于每次更新，按顺序执行以下操作，并输出此时的 $f(A)$ 值：

将 $A_{X_i}$ 更改为 $Y_i$。

题目描述

样例输入 #1

4 2 10
1 5
2 1
3 3
4 2
2 10
1 0
4 0
3 1
2 0
3 0

样例输出 #1

5
6
8
8
15
13
13
11
1
0

提示

• $1\ \le\ K\ \le\ N\ \le\ 5\ \times\ 10^5$
• $1\ \le\ Q\ \le\ 5\ \times\ 10^5$
• $1\ \le\ X_i\ \le\ N$
• $0\ \le\ Y_i\ \le\ 10^9$

思路

可以使用对顶堆,这里涉及到修改操作，因此可以使用multiset维护方便一些

• a维护前k大为小根堆
• b维护比第k个数小的，大根堆

使用res来维护前k大的和。

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

const int N = 5e5 + 10;
int n, k, q, res;
int w[N];
multiset<int> a, b;

//a维护前k大，小根堆    b维护比第k个数小的，大根堆
void solve() {
    cin >> n >> k >> q;
    for (int i = 1; i <= k; i++)a.insert(0);
    for (int i = 1; i <= n - k; i++) b.insert(0);
    while (q--) {
        int x, y;
        cin >> x >> y;
        if (a.find(w[x]) != a.end()) a.erase(a.find(w[x])), res -= w[x];
        else b.erase(b.find(w[x]));
        w[x] = y;
        if (!b.empty() && y >= *b.rbegin()) a.insert(y), res += y;
        else b.insert(y);
        while (a.size() > k) {
            b.insert(*a.begin());
            res -= *a.begin();
            a.erase(a.begin());
        }
        while (a.size() < k) {
            a.insert(*b.rbegin());
            res += *b.rbegin();
            b.erase(b.find(*b.rbegin()));
        }
        cout << res << endl;
    }
}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    while (_--) solve();
    return 0;
}