线段树

线段树介绍

线段树树基于分治思想的二叉树，用来维护区间信息(区间和、区间最大值、区间最小值等等)。可以在$O(logn)$的时间内完成区间信息的查询和修改。

• 线段树中每个叶子结点存储元素本身，非叶子结点存储区间内元素的统计值

节点数组tr[]

l,r存区间的左右端点，sum存区间和

int n,w[N];
struct node{
  int l,r,sum;
}tr[N*4];//注意需要开四倍空间

递归建树

父节点的编号为p

左孩子编号为2*p,右孩子编号为2*p+1

#define lc p<<1
#define rc p<<1|1 或者2*p+1

void build(int p,int l,int r){
  tr[p]={l,r,w[l]};
  if(l==r) return;//是叶子结点了，直接返回
  int mid=l+r>>1;
  build(lc,l,mid);
  build(rc,mid+1,r);
  tr[p].sum=tr[lc].sum+tr[rc].sum;
}

单点修改

从根节点进入，递归找到叶子结点[x,x],把该结点的值增加k，然后从下往上更新其祖先节点上的统计值。

void update(int p,int x,int k){//将x位置上的数加k
  if(tr[p].l==x && tr[p].r==x){
    tr[p].sum+=k;
    return;
  }
  int mid=l+r>>1;
  if(x<=mid) update(lc,x,k); //只会进入一个分支
  else update(rc,x,k);
  tr[p].sum=tr[lc].sum+tr[rc].sum;
}

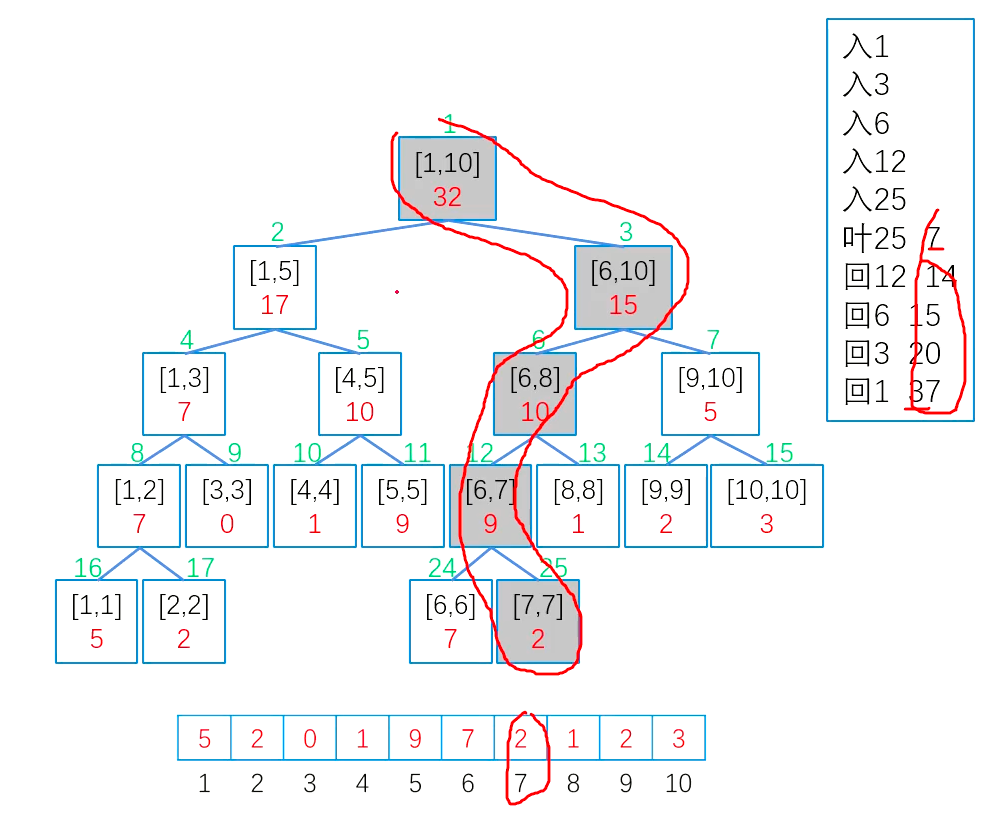
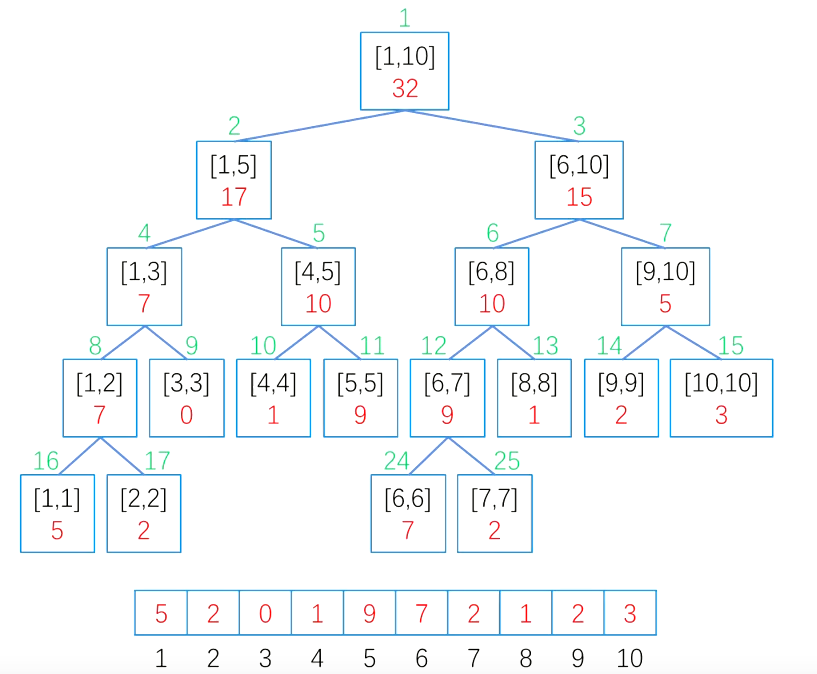
区间查询

区间查询使用拆分和拼凑的思想，例如，查询区间[4,9]可以拆分为[4,5],[6,8],[9,9]，通过合并这三个区间的答案来求查询的答案。

从根节点进入，递归执行以下过程：

1. 若查询区间[x,y]完全覆盖当前区间，则立即回溯，并返回该结点的sum值
2. 若左子节点与[x,y]有重叠，则递归访问左子树
3. 若右子节点与[x,y]有重叠，则递归访问右子树

int query(int p,int x,int y){
  if(x<=tr[p].l &&tr[p].r<=y)return tr[p].sum;
  int mid=tr[p].l+tr[p].r>>1;
  int sum=0;
  if(x<=mid) sum+=query(lc,x,y);
  if(y>mid) sum+=query(rc,x,y);
  return sum;
}

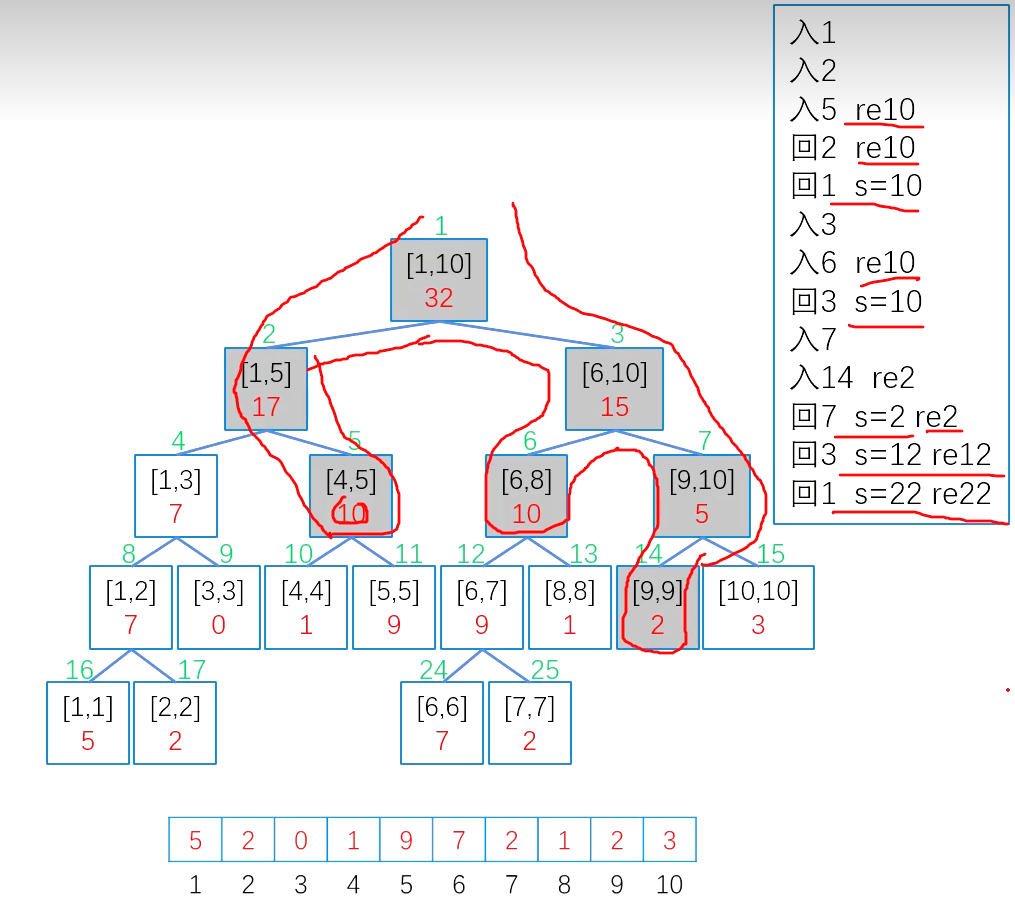
区间修改

例如对区间[4,5]内的每个数加上5，如果修改区间[x,y]所覆盖的每个叶子结点，时间是$O(n)$的

可以做懒惰修改，当[x,y]完全覆盖节点区间[a,b]时，先修改区间的sum值，然后打上一个懒标记，然后立即返回，等下次需要的时候，再下传懒标记，这样可以把修改和查询的时间都控制在$O(logn)$内

void pushup(int p){
  tr[p].sum=tr[lc].sum+tr[rc].sum;
}

void pushdown(int p){
  if(tr[p].add){
    tr[lc].sum+=tr[p].add* (tr[lc].r-tr[lc].l+1);
    tr[rc].sum+=tr[p].add* (tr[rc].r-tr[rc].l+1);
    tr[lc].add+=tr[p].add;
    tr[rc].add+=tr[p].add;
    tr[p].add=0;
  }
}

void update(int p,int x,int y,int k){
  if(x<=tr[p].l &&tr[p].r<=y){
    tr[p].sum+=(tr[p].r-tr[p].l+1)*k;
    tr[p].add+=k;
    return;
  }
  int m=tr[p].l+tr[p].r>>1;
  pushdown(p);
  if(x<=m) update(lc,x,y,k);
  if(y>m) update(rc,x,y,k);
  pushup(p);
}

【模板】树状数组 1

链接：https://www.luogu.com.cn/problem/P3374

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 $x$

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 $x$ 个数加上 $k$

• 2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

14
16

提示

【数据范围】

对于 $30\%$ 的数据，$1 \le n \le 8$，$1\le m \le 10$；
对于 $70\%$ 的数据，$1\le n,m \le 10^4$；
对于 $100\%$ 的数据，$1\le n,m \le 5\times 10^5$。

代码

#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define debug(s, x) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

#define lc p << 1
#define rc p << 1 | 1
const int N = 5e5 + 10;

struct tr {
    int l, r, sum;
} tr[N * 4];
int w[N];
void build(int p, int l, int r) {
    tr[p] = {l, r, w[l]};
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    tr[p].sum = tr[lc].sum + tr[rc].sum;
}

void update(int p, int x, int k) {
    if (tr[p].l == x && tr[p].r == x) {
        tr[p].sum += k;
        return;
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    if (x <= mid)
        update(lc, x, k);
    else
        update(rc, x, k);
    tr[p].sum = tr[lc].sum + tr[rc].sum;
}

int query(int p, int x, int y) {
    if (x <= tr[p].l && tr[p].r <= y) {
        return tr[p].sum;
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    int sum = 0;
    if (x <= mid)
        sum += query(lc, x, y);
    if (y > mid)
        sum += query(rc, x, y);
    return sum;
}

void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    build(1, 1, n);
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        if (a == 1)
            update(1, b, c);
        else
            cout << query(1, b, c) << endl;
    }
}

signed main() {
    int _=1;
    while (_--)
        solve();
    return 0;
}

【模板】线段树 1

链接：https://www.luogu.com.cn/problem/P3372

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 $k$。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n, m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

1. 1 x y k：将区间 $[x, y]$ 内每个数加上 $k$。
2. 2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例输入 #1

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

样例输出 #1

11
8
20

提示

对于 $30\%$ 的数据：$n \le 8$，$m \le 10$。
对于 $70\%$ 的数据：$n \le {10}^3$，$m \le {10}^4$。
对于 $100\%$ 的数据：$1 \le n, m \le {10}^5$。

保证任意时刻数列中所有元素的绝对值之和 $\le {10}^{18}$。

代码

#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define debug(s, x) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

#define lc p * 2
#define rc p * 2 + 1

const int N = 1e5 + 10;
int n, m;

struct tr {
    int l, r, sum, add;
} tr[N * 4];
int w[N];

void pushup(int p) {
    tr[p].sum = tr[lc].sum + tr[rc].sum;
}

void pushdown(int p) {
    if (tr[p].add) {
        tr[lc].sum += tr[p].add * (tr[lc].r - tr[lc].l + 1);
        tr[rc].sum += tr[p].add * (tr[rc].r - tr[rc].l + 1);
        tr[lc].add += tr[p].add;
        tr[rc].add += tr[p].add;
        tr[p].add = 0;
    }
}

void build(int p, int l, int r) {
    tr[p] = {l, r, w[l], 0};
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    pushup(p);
}

void update(int p, int x, int y, int k) {
    if (x <= tr[p].l && tr[p].r <= y) {
        tr[p].sum += (tr[p].r - tr[p].l + 1) * k;
        tr[p].add += k;
        return;
    }
    pushdown(p);
    int mid = (tr[p].l + tr[p].r) >> 1;
    if (x <= mid)
        update(lc, x, y, k);
    if (y > mid)
        update(rc, x, y, k);
    pushup(p);
}

int query(int p, int x, int y) {
    if (x <= tr[p].l && tr[p].r <= y) {
        return tr[p].sum;
    }
    pushdown(p);
    int mid = (tr[p].l + tr[p].r) >> 1;
    int res = 0;
    if (x <= mid)
        res += query(lc, x, y);
    if (y > mid)
        res += query(rc, x, y);
    pushup(p);
    return res;
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    build(1, 1, n);
    while (m--) {
        int op;
        cin >> op;
        if (op == 1) {
            int x, y, k;
            cin >> x >> y >> k;
            update(1, x, y, k);
        } else {
            int x, y;
            cin >> x >> y;
            cout << query(1, x, y) << endl;
        }
    }
}
signed main() {
    int _ = 1;
    while (_--)
        solve();
    return 0;
}

最大数

题目描述

链接：https://www.acwing.com/problem/content/1277/

给定一个正整数数列 $a_1,a_2,…,a_n$，每一个数都在 $0 \sim p-1$ 之间。

可以对这列数进行两种操作：

1. 添加操作：向序列后添加一个数，序列长度变成 $n+1$；
2. 询问操作：询问这个序列中最后 $L$ 个数中最大的数是多少。

程序运行的最开始，整数序列为空。

一共要对整数序列进行 $m$ 次操作。

写一个程序，读入操作的序列，并输出询问操作的答案。

输入格式

第一行有两个正整数 $m,p$，意义如题目描述；

接下来 $m$ 行，每一行表示一个操作。

如果该行的内容是 Q L，则表示这个操作是询问序列中最后 $L$ 个数的最大数是多少；

如果是 A t，则表示向序列后面加一个数，加入的数是 $(t+a)\ mod\ p$。其中，$t$ 是输入的参数，$a$ 是在这个添加操作之前最后一个询问操作的答案（如果之前没有询问操作，则 $a=0$）。

第一个操作一定是添加操作。对于询问操作，$L>0$ 且不超过当前序列的长度。

输出格式

对于每一个询问操作，输出一行。该行只有一个数，即序列中最后 $L$ 个数的最大数。

数据范围

$1 \le m \le 2 \times 10^5$,
$1 \le p \le 2 \times 10^9$,
$0 \le t < p$

输入样例：

10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99

输出样例：

97
97
97
60
60
97

样例解释

最后的序列是 $97,14,60,96$。

思路

因为一开始序列的长度不知道是多少，但是最多m个询问，最坏情况下数组长度就为m呗，初始化的时候就可以建立1,m的线段树

然后使用线段树维护区间的最大值，使用n记录此时数组的长度，每次添加操作，n就加1

代码

#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define debug(s, x) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

#define lc p << 1
#define rc p << 1 | 1

const int N = 2e5 + 10;

int n = 1, m, p, a;

struct node {
    int l, r, sum;
} tr[N * 4];

void pushdown(int p) {
    tr[p].sum = max(tr[lc].sum, tr[rc].sum);
}

void build(int p, int l, int r) {
    tr[p] = {l, r, 0};
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
}

void update(int p, int x, int k) {
    if (tr[p].l == x && tr[p].r == x) {
        tr[p].sum = k;
        return;
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    if (x <= mid)
        update(lc, x, k);
    else
        update(rc, x, k);
    pushdown(p);
}

int query(int p, int x, int y) {
    if (x <= tr[p].l && tr[p].r <= y) {
        return tr[p].sum;
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    int res = 0;
    if (x <= mid)
        res = max(res, query(lc, x, y));
    if (y > mid)
        res = max(res, query(rc, x, y));
    return res;
}

void solve() {
    cin >> m >> p;
    build(1, 1, m);
    while (m--) {
        char op;
        int x;
        cin >> op >> x;
        if (op == 'A') {
            update(1, n, (a + x) % p);
            n++;
        } else {
            a = query(1, n - x, n - 1);
            cout << a << endl;
        }
    }
}
signed main() {
    int _ = 1;
    while (_--)
        solve();
    return 0;
}

你能回答这些问题吗

题目描述

链接：https://www.acwing.com/problem/content/description/246/

给定长度为 $N$ 的数列 $A$，以及 $M$ 条指令，每条指令可能是以下两种之一：

1. 1 x y，查询区间 $[x,y]$ 中的最大连续子段和，即 $\max\limits_{x \le l \le r \le y}$ $\sum\limits^r_{i=l} A[i]$。
2. 2 x y，把 $A[x]$ 改成 $y$。

对于每个查询指令，输出一个整数表示答案。

输入格式

第一行两个整数 $N,M$。

第二行 $N$ 个整数 $A[i]$。

接下来 $M$ 行每行 $3$ 个整数 $k,x,y$，$k=1$ 表示查询（此时如果 $x>y$，请交换 $x,y$），$k=2$ 表示修改。

输出格式

对于每个查询指令输出一个整数表示答案。

每个答案占一行。

数据范围

$N \le 500000, M \le 100000$,
$-1000 \le A[i] \le 1000$

输入样例：

5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2

输出样例：

2
-1

思路

用线段树维护区间最大的连续子段和：

• $sum$记录区间$[l,r]$的和
• $lmax$记录区间$[l,r]$的从$l$开始的最大连续子段和
• $rmax$记录区间$[l,r]$的从$r$开始的最大连续子段和
• $max$记录区间$[l,r]$的最大连续子段和

在更新父节点的这些数据时，有：

• $tr[p].sum = tr[lc].sum + tr[rc].sum;$

父节点的区间和就是两个子节点的区间和之和

• $tr[p].lmax = max(tr[lc].lmax, tr[lc].sum + tr[rc].lmax);$

父节点从左开始的最大连续子段和为 max(左儿子从左开始的最大连续字段和，左孩子的区间和+右儿子从左开始的最大连续子段和)

• $tr[p].rmax = max(tr[rc].rmax, tr[rc].sum + tr[lc].rmax);$
• $tr[p].max = max(max(tr[lc].max, tr[rc].max), tr[lc].rmax + tr[rc].lmax);$

父节点的区间最大连续字段和为 左儿子的右连续区间和+右儿子的左连续区间和 以及左右儿子各自最大连续区间和取最大值。

代码

#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define debug(s, x) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;
#define lc p << 1
#define rc p << 1 | 1

const int N = 5e5 + 10;
int n, m;
int w[N];
struct node {
    int l, r, sum, lmax, rmax, max;
} tr[N * 4];

void pushdown(int p) {
    tr[p].sum = tr[lc].sum + tr[rc].sum;
    tr[p].lmax = max(tr[lc].lmax, tr[lc].sum + tr[rc].lmax);
    tr[p].rmax = max(tr[rc].rmax, tr[rc].sum + tr[lc].rmax);
    tr[p].max = max(max(tr[lc].max, tr[rc].max), tr[lc].rmax + tr[rc].lmax);
}

void build(int p, int l, int r) {
    tr[p] = {l, r, w[l], w[l], w[l], w[l]};
    if (l == r)
        return;
    int mid = (l + r) >> 1;
    build(lc, l, mid);
    build(rc, mid + 1, r);
    pushdown(p);
}

void update(int p, int x, int k) {
    if (tr[p].l == x && tr[p].r == x) {
        tr[p] = {x, x, k, k, k, k};
        return;
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    if (x <= mid)
        update(lc, x, k);
    else
        update(rc, x, k);
    pushdown(p);
}

node query(int p, int x, int y) {
    if (x <= tr[p].l && tr[p].r <= y) {
        return tr[p];
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    if (y <= mid)
        return query(lc, x, y);
    if (x > mid)
        return query(rc, x, y);
    node left = query(lc, x, y);
    node right = query(rc, x, y);
    node t;
    t.sum = left.sum + right.sum;
    t.lmax = max(left.lmax, left.sum + right.lmax);
    t.rmax = max(right.rmax, right.sum + left.rmax);
    t.max = max(max(left.max, right.max), right.lmax + left.rmax);
    return t;
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    build(1, 1, n);
    int op, x, y;
    while (m--) {
        cin >> op >> x >> y;
        if (op == 1) {
            if (x > y)
                swap(x, y);
            cout << query(1, x, y).max << endl;
        } else
            update(1, x, y);
    }
}
signed main() {
    int _ = 1;
    while (_--)
        solve();
    return 0;
}